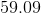To solve, simply multiply the side length by 3 since they are all equal. Thus,

Draw out 3 radii and 3 lines to the corners of each triangle, creating 6 30-60-90 triangles.

See that these 30-60-90 triangles can be used to find side length.

Formula for side of equilateral triangle is

.

Now substitute the new equation that is in terms of R in for S.

Draw 3 radii, and then 3 new lines that bisect the radii. You get six 30-60-90 triangles.

These triangles can be used ot find a side length .

Using the formula for the area of an equilateral triangle in terms of its side, we get

The Pythagorean Theorem states that . This question gives us the values of and , and asks us to solve for .

Take and and plug them into the equation as and :

Now we can start solving for :

The length of the hypotenuse is .

To solve, simply use the Pythagorean Theorem.

Recall that an isosceles right triangle has two leg lengths that are equal.

Therefore, to solve for the hypotenuse let and in the Pythagorean Theorem.

Thus,

To solve, simply multiply the side length by 3 since they are all equal. Thus,

To solve, simply multiply the side length by . Thus,

Draw 3 radii, and then 3 new lines that bisect the radii. You get six 30-60-90 triangles.

These triangles can be used ot find a side length .

Using the formula for the area of an equilateral triangle in terms of its side, we get

Draw out 3 radii and 3 lines to the corners of each triangle, creating 6 30-60-90 triangles.

See that these 30-60-90 triangles can be used to find side length.

Formula for side of equilateral triangle is

.

Now substitute the new equation that is in terms of R in for S.

Begin by filling in the missing angle for your triangle. Since a triangle has a total of degrees, you know that the missing angle is:

Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:

Solving for , you get:

Rounding, this is .