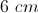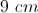Acute / Obtuse Isosceles Triangles
Help Questions
ACT Math › Acute / Obtuse Isosceles Triangles
What is the height of an isosceles triangle which has a base of 

Explanation
The area of a triangle is given by the equation:
In this case, we are given the area (


To do this, we must plug in the given values for 

We then must multiply the right side, and then divide the entire equation by 2, in order to solve for 
Therefore, the height of the triangle is 
What is the height of an isosceles triangle which has a base of 

Explanation
The area of a triangle is given by the equation:
In this case, we are given the area (


To do this, we must plug in the given values for 

We then must multiply the right side, and then divide the entire equation by 2, in order to solve for 
Therefore, the height of the triangle is 
The base angle of an isosceles triangle is thirteen more than three times the vertex angle. What is the difference between the vertex angle and the base angle?
Explanation
Every triangle has 
Let 

The equation to solve becomes 
Now we can solve for the vertex angle.
The difference between the vertex angle and the base angle is 
The base angle of an isosceles triangle is thirteen more than three times the vertex angle. What is the difference between the vertex angle and the base angle?
Explanation
Every triangle has 
Let 

The equation to solve becomes 
Now we can solve for the vertex angle.
The difference between the vertex angle and the base angle is 
An isosceles triangle has a base of 

Explanation

An isosceles triangle has a base of 

Explanation

In the standard 


Explanation
To form an isosceles triangle here, we need to create a third vertex whose 






Triangle FGH has equal lengths for FG and GH; what is the measure of ∠F, if ∠G measures 40 degrees?
140 degrees
70 degrees
40 degrees
100 degrees
None of the other answers
Explanation
It's good to draw a diagram for this; we know that it's an isosceles triangle; remember that the angles of a triangle total 180 degrees.
Angle G for this triangle is the one angle that doesn't correspond to an equal side of the isosceles triangle (opposite side to the angle), so that means ∠F = ∠H, and that ∠F + ∠H + 40 = 180,
By substitution we find that ∠F * 2 = 140 and angle F = 70 degrees.
In the standard 


Explanation
To form an isosceles triangle here, we need to create a third vertex whose 






Triangle FGH has equal lengths for FG and GH; what is the measure of ∠F, if ∠G measures 40 degrees?
140 degrees
70 degrees
40 degrees
100 degrees
None of the other answers
Explanation
It's good to draw a diagram for this; we know that it's an isosceles triangle; remember that the angles of a triangle total 180 degrees.
Angle G for this triangle is the one angle that doesn't correspond to an equal side of the isosceles triangle (opposite side to the angle), so that means ∠F = ∠H, and that ∠F + ∠H + 40 = 180,
By substitution we find that ∠F * 2 = 140 and angle F = 70 degrees.