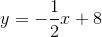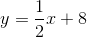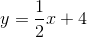ACT Math - How to graph a line

What is the distance between (7, 13) and (1, 5)?

None of the answers are correct

Explanation

The distance formula is given by d = square root \[(x2 – x1)2 + (y2 – y1)2\]. Let point 2 be (7,13) and point 1 be (1,5). Substitute the values and solve.

What is the midpoint between and ?

None of the answers are correct

Explanation

The x-coordinate for the midpoint is given by taking the arithmetic average (mean) of the x-coordinates of the two end points. So the x-coordinate of the midpoint is given by $(1+7)\div2=4$

The same procedure is used for the y-coordinates. So the y-coordinate of the midpoint is given by $(5+3)\div2=4$

Thus the midpoint is given by the ordered pair

What is the slope of this line? Screen_shot_2013-07-13_at_5.10.26_pm

$\frac{1}{2}$

$-\frac{1}{2}$

Explanation

The slope is found using the formula $m=\frac{y_2-y_1}{x_2-x_1}$ .

We know that the line contains the points (3,0) and (0,6). Using these points in the above equation allows us to calculate the slope.

$\frac{6-0}{0-3}=\frac{6}{-3}=-2$

Axes

Refer to the above diagram. If the red line passes through the point $\left ( N, 4\right )$ , what is the value of ?

$N = -4\frac{2}{3}$

$N= -1\frac{1}{3}$

$N = -7\frac{1}{3}$

$N = -3\frac{1}{3}$

Explanation

One way to answer this is to first find the equation of the line.

The slope of a line. given two points $(x_{1}, y_{1}), (x_{2}, y_{2})$ can be calculated using the slope formula

$m = \frac{y_{2}-y_{1}}{x_{2}-x _{1}}$

Set $x_{1}=-6, y_{1}=x_{2}= 0, y_{2}=18$ :

$m = \frac{18-0}{0-(-6)} = \frac{18}{6} = 3$

The line has slope 3 and -intercept , so we can substitute in the slope-intercept form:

Now substitute 4 for and for and solve for :

$N = -\frac{14}{3}= -4\frac{2}{3}$

Line

Refer to the above red line. A line is drawn perpendicular to that line, and with the same -intercept. Give the equation of that line in slope-intercept form.

$y = - \frac{1}{2}x + 8$

$y = \frac{1}{2}x + 8$

$y = - \frac{1}{2}x + 4$

$y = \frac{1}{2}x + 4$

$y = \frac{1}{2}x - 4$

Explanation

First, we need to find the slope of the above line.

The slope of a line. given two points $(x_{1}, y_{1}), (x_{2}, y_{2})$ can be calculated using the slope formula

$m = \frac{y_{2}-y_{1}}{x_{2}-x _{1}}$

Set $x_{1}=-4, y_{1}=x_{2}= 0, y_{2}=8$ :

$m = \frac{8-0}{0-(-4)} = \frac{8}{4} = 2$

The slope of a line perpendicular to it has as its slope the opposite of the reciprocal of 2, which would be $m = -\frac{1}{2}$ . Since we want this line to have the same -intercept as the first line, which is the point , we can substitute $m = -\frac{1}{2}$ and in the slope-intercept form: