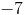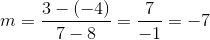ACT Math - How to find the slope of a line

What is the slope of a line which passes through coordinates $\dpi{100} \small (3,7)$ and $\dpi{100} \small (4,12)$ ?

$\dpi{100} \small 5$

$\dpi{100} \small \frac{1}{5}$

$\dpi{100} \small \frac{1}{2}$

$\dpi{100} \small 2$

$\dpi{100} \small 3$

Explanation

Slope is found by dividing the difference in the $\dpi{100} \small y$ -coordinates by the difference in the $\dpi{100} \small x$ -coordinates.

$\dpi{100} \small \frac{(12-7)}{(4-3)}=\frac{5}{1}=5$

What is the slope of a line that passes though the coordinates $(5,2)$ and $(3,1)$ ?

$\frac{1}{2}$

$-\frac{1}{2}$

$-\frac{2}{3}$

$\frac{2}{3}$

$4$

Explanation

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{1-2}{3-5}=\frac{-1}{-2}=\frac{1}{2}$

What is the slope of a line running through points and ?

$-\frac{1}{7}$

$\frac{7}{3}$

Explanation

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{3-(-4)}{7-8}=\frac{7}{-1}=-7$

What is the slope of the line defined by the equation ?

$-\frac{3}{4}$

$\frac{4}{3}$

$\frac{1}{3}$

Explanation

The easiest way to find the slope of a line based on its equation is to put it into the form . In this form, you know that is the slope.

Start with your original equation .

Now, subtract from both sides:

Next, subtract from both sides:

Finally, divide by :

$y = 5-\frac{3}{4}x$

This is the same as:

$y = -\frac{3}{4}x + 5$

Thus, the slope is $-\frac{3}{4}$ .

What is the slope of the line defined as ?

$\frac{-3}{4}$

$\frac{-4}{3}$

$\frac{4}{3}$

$\frac{11}{2}$

$\frac{-2}{11}$

Explanation

To calculate the slope of a line from an equation of the line, the easiest way to proceed is to solve it for . This will put it into the format , making it very easy to find the slope . For our equation, it is:

Next you merely need to divide by :

$y = \frac{-3}{4}x+\frac{22}{4}$

Thus, the slope is $\frac{-3}{4}$

What is the slope of the line perpendicular to ?

$\frac{1}{2}$

$\frac{44}{3}$

$\frac{-1}{11}$

Explanation

To begin, it is easiest to find the slope of a line by putting it into the form . is the slope, so you can immediately find this once you have the format correct. Thus, solve our equation for :

Now, recall that perpendicular lines have slopes of opposite sign and reciprocal numerical value. Thus, if our slope is , its perpendicular paired line will have a slope of $\frac{1}{2}$ .

What is the slope of the line represented by the equation ?

Explanation

The slope of an equation can be calculated by simplifying the equation to the slope-intercept form , where m=slope.

Since , we can solve for y. In shifting the 5 to the other side, we are left with .

This can be further simplified to

$y = 3x + \frac{5}{4}$ , leaving us with the slope intercept form.

In this scenario, , so slope .

If 2x – 4y = 10, what is the slope of the line?

–5/2

–0.5

0.5

–2

Explanation

First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.

What is the slope of the line with equation 4_x_ – 16_y_ = 24?

1/4

1/8

–1/4

–1/8

1/2

Explanation

The equation of a line is:

y = mx + b, where m is the slope

4_x_ – 16_y_ = 24

–16_y_ = –4_x_ + 24

y = (–4_x_)/(–16) + 24/(–16)

y = (1/4)x – 1.5

Slope = 1/4

What is the slope of the line represented by the equation $6y-16x=7$ ?

$\frac{8}{3}$

$\frac{7}{6}$

$16$

$6$

$-16$

Explanation

To rearrange the equation into a $y=mx+b$ format, you want to isolate the $y$ so that it is the sole variable, without a coefficient, on one side of the equation.

First, add $11x$ to both sides to get $6y=7+16x$ .

Then, divide both sides by 6 to get $y=\frac{7+16x}{6}$ .

If you divide each part of the numerator by 6, you get $y=\frac{7}{6}+\frac{16x}{6}$ . This is in a $y=b+mx$ form, and the $m$ is equal to $\frac{16}{6}$ , which is reduced down to $\frac{8}{3}$ for the correct answer.

How to find the slope of a line

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation