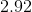ACT Math - How to find a missing side with cosine

A man has a rope that is $40\textup{ feet}$ long, attached to the top of a small building. He pegs the rope into the ground at an angle of $14.5$^{\circ}$$ . How far away from the building did he walk horizontally to attach the rope to the ground? Round to the nearest inch.

$38\textup{ feet and }9\textup{ inches}$

$10\textup{ feet}$

$12\textup{ feet and }4\textup{ inches}$

$10\textup{ feet and 4 inches}$

$37\textup{ feet and 5 inches}$

Explanation

Begin by drawing out this scenario using a little right triangle:

Cos30

We know that the cosine of an angle is equal to the ratio of the side adjacent to that angle to the hypotenuse of the triangle. Thus, for our triangle, we know:

$cos(14.5) =\frac{x}{40}$

Using your calculator, solve for :

This is . Now, take the decimal portion in order to find the number of inches involved.

Thus, rounded, your answer is feet and inches.

Cos75

What is $\small x$ in the right triangle above? Round to the nearest hundredth.

$\small 369.58$

$\small 63.51$

$\small 64.44$

$\small 264.52$

$\small 355.83$

Explanation

Recall that the cosine of an angle is the ratio of the adjacent side to the hypotenuse of that triangle. Thus, for this triangle, we can say:

$\small cos(9.75)=\frac{x}{375}$

Solving for $\small x$ , we get:

$\small 375*cos(9.75)=x$

$\small x=369.58352214677914$ or $\small 369.58$

The hypotenuse of right triangle HLM shown below is long. The cosine of angle is $\frac{2}{5}$ . How many inches long is ?

Explanation

Remember that $\cos\theta=\frac{adjacent}{hypotenuse}$

Then, we can set up the equation using the given information.

$\cos H=\frac{HL}{19}=\frac{2}{5}$

Now, solve for .

$HL=\frac{38}{5}=7.6$

$\textup{If}\ cos(\theta)=\frac{16}{20}$

$\textup{then}\ sin(\theta)=$

$\frac{3}{5}$

$\frac{4}{5}$

$\frac{9}{20}$

$\frac{13}{20}$

$\frac{2}{5}$

Explanation

To solve this problem you need to make the triangle that the problem is talking about. Cosine is equal to the adjacent side over the hypotenuse of a right triangle

$cos(\theta)=\frac{adj}{hyp}$

So this is what our triangle looks like:

Triangle_3

Now use the pythagorean theorem to find the other side:

Sine is equal to the opposite side over the hypotenuse, the opposite side is 12

$sin(\theta)=\frac{opp}{hyp}$

$sin(\theta)=\frac{12}{20}=\frac{3}{5}$

Triangle

If angle A measures 30 degrees and the hypotenuse is 4, what is the length of AB in the given right triangle?

2√3

√3

8√3

Explanation

Cosine A = Adjacent / Hypotenuse = AB / AC = AB / 4

Cosine A = AB / 4

Cos (30º) = √3 / 2 = AB / 4

Solve for AB

√3 / 2 = AB / 4

AB = 4 * (√3 / 2) = 2√3

Right triangle

In the right triangle shown above, what is the $\cos\left (A \right )$ ?

$\frac{b}{c}$

$\frac{a}{c}$

$\frac{b}{a}$

$\frac{a}{b}$

$\frac{c}{a}$

Explanation

Use SOH-CAH-TOA to solve for the sine of a given angle. This stands for:

$\sin = \frac{\textup{opposite}}{\textup{hypotenuse}}$

$\cos = \frac{\textup{adjacent}}{\textup{hypotenuse}}$

$\tan = \frac{\textup{opposite}}{\textup{adjacent}}$ .

From our triangle we see that at point , the adjacent side is side and the hypotenuse doesn't depend upon position, it's always . Thus we get that $cos(A)=\frac{b}{c}$

Right triangle

In a given right triangle $\Delta ABC$ , hypotenuse and $\angle A = 42^{\circ}$ . Using the definition of $\cos$ , find the length of leg . Round all calculations to the nearest tenth.

Explanation

In right triangles, SOHCAHTOA tells us that $\cos A =\frac{\textup{adjacent}}{\textup{hypotenuse}}$ , and we know that $\angle A = 42^{\circ}$ and hypotenuse . Therefore, a simple substitution and some algebra gives us our answer.

$\cos 42^{\circ} = \frac{AB}{25}$

$.7 = \frac{AB}{25}$ Use a calculator or reference to approximate cosine.

Isolate the variable term.

Thus, .

In a given right triangle $\Delta ABC$ , hypotenuse and $\angle A = 66^{\circ}$ . Using the definition of $\cos$ , find the length of leg . Round all calculations to the nearest hundredth.

Explanation

In right triangles, SOHCAHTOA tells us that $\cos A = \frac{\textup{adjacent}}{\textup{hypotenuse}}$ , and we know that $A = 66^{\circ}$ and hypotenuse . Therefore, a simple substitution and some algebra gives us our answer.

$\cos 66^{\circ} = \frac{AB}{8}$

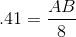
$.41 = \frac{AB}{8}$ Use a calculator or reference to approximate cosine.

Isolate the variable term.

Thus, .

An airline pilot must know the exact vertical height of his plane above the runway to know when to extend the landing gear under the nose. If the nose of the plane is feet away from the ground and the plane is descending at an angle of $75 ^{\circ}$ to the vertical, how far above the ground to the nearest foot is the landing gear?

(Ignore the height of the plane itself).

Explanation

The plane itself is effectively at the top of a right triangle, with topmost angle $75^{\circ}$ and hypotenuse feet. If this is the case, then SOHCAHTOA tells us that $\textup{cos} (75)^{\circ} = \frac{\textup{adjacent}}{\textup{hypotenuse}} = \frac{x}{43}$ .

Now, solve for the adjacent:

$x = \textup{cos}(75^{\circ}) \cdot 43 \approx 11.13$

Thus, our plane's nose is approximately feet from the runway.

In a given right triangle $\Delta ABC$ , hypotenuse and $\angle C = 75^{\circ}$ . Using the definition of $\cos$ , find the length of leg . Round all calculations to the nearest tenth.

Explanation

In right triangles, SOHCAHTOA tells us that $\cos C = \frac{\textup{adjacent}}{\textup{hypotenuse}}$ , and we know that $A = 75^{\circ}$ and hypotenuse . Therefore, a simple substitution and some algebra gives us our answer.