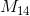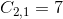Operations and Properties

Help Questions

Linear Algebra › Operations and Properties

Questions 1 - 10

Consider the matrix

$A = \begin{bmatrix} -1&4 &1 \ -2& 3& 1\ 1&6 & 2 \end{bmatrix}$ .

Give cofactor $C_{33}$ of this matrix.

$C_{33}= 5$

$C_{33}=- 5$

$C_{33}= -11$

$C_{33}= 11$

$C_{33}= 0$

Explanation

The minor of a matrix $M_{mn}$ is the determinant of the matrix formed by striking out Row and Column . By definition, the corresponding cofactor $C_{mn}$ can be calculated from this minor using the formula

$C_{mn}= ( -1 )^{m+n} M_{mn}$

To find cofactor $C_{33}$ , we first find minor $M_{33}$ by striking out Row 3 and Column 3, as follows:

Minor

$M_{33}$ is equal to the determinant

$\begin{vmatrix} -1& 4\-2& 3 \end{vmatrix}$

which is found by taking the product of the upper left and lower right entries and subtracting that of the other two entries:

$M_{33} = (-1)(3)- 4 (-2) = -3 -(-8)= 5$

In the cofactor equation, set :

$C_{33}= ( -1 )^{3+3 } M_{33} = ( -1 )^{6 } \cdot 5 = 1 \cdot 5 = 5$

$\begin{align*}&\text{Find any and all eigenvalues for the matrix }\&A=\begin{bmatrix}-9&-2\-2&-2\end{bmatrix}\end{align*}$

$\lambda_{1}=-9.53;\lambda_{2}=-1.47$

$\lambda_{1}=-12.53;\lambda_{2}=-4.47$

$\lambda_{1}=-15.53;\lambda_{2}=-7.47$

$\lambda_{1}=-0.53;\lambda_{2}=7.53$

Explanation

$\begin{align*}&\text{Eigenvalues of a matrix, typically noted as }\lambda\text{, are those values which satisfy}\&det(A-\lambda I)\text{(I being the identity matrix). For the matrix }A=\begin{bmatrix}-9&-2\-2&-2\end{bmatrix}\&\text{We can represent that equation as follows }\begin{bmatrix}- \lambda - 9&-2\-2&- \lambda - 2\end{bmatrix}\&\text{For a square matrix with dimensions of }2\&det\begin{vmatrix} a&b \ c&d \end{vmatrix}=ad-bc\&\text{From that, we can find the eigenvalues:}\&11\lambda + \lambda ^{2} + 14\&\lambda_{1}=-9.53;\lambda_{2}=-1.47\end{align*}$

Let be a four-by-four matrix.

Cofactor $C_{13}$ must be equal to:

Minor $M_{13}$

The additive inverse of Minor $M_{14}$

The reciprocal of Minor $M_{14}$

The additive inverse of the reciprocal of Minor $M_{14}$

None of the other choices gives a correct response.

Explanation

$C_{mn}= ( -1 )^{m+n} M_{mn}$

Set ; the formula becomes

$C_{13}= ( -1 )^{1+3} M_{13}$

$C_{13}= ( -1 )^{ 4} M_{13}$

$C_{13}=1 \cdot M_{13}$

$C_{13}= M_{13}$ ,

making the quantities equal.

Consider the matrix

$A = \begin{bmatrix} -1&4 &1 \ -2& 3& 1\ 1&6 & 2 \end{bmatrix}$ .

Give cofactor $C_{2 3}$ of this matrix.

$C_{23} = 10$

$C_{23} = -10$

$C_{23} = 2$

$C_{23} = -2$

$C_{23} = 0$

Explanation

$C_{mn}= ( -1 )^{m+n} M_{mn}$

To find cofactor $C_{2 3}$ , we first find minor $M_{23}$ by striking out Row 2 and Column 3, as follows:

Minor

$M_{23}$ is equal to the determinant

$\begin{vmatrix} -1& 4\ 1& 6 \end{vmatrix}$

which is found by taking the product of the upper left and lower right entries and subtracting that of the other two entries:

$M_{23} = -1(6)- 1(4) = -6 - 4 = -10$

In the cofactor equation, set :

$C_{23}= ( -1 )^{2+3} M_{23}= ( -1 )^{5} (-10) = (-1)(-10) = 10$

True or False: If a $5 \times 5$ matrix has linearly independent columns, then .

True

False

Explanation

Since is a $5 \times 5$ matrix, . Since has three linearly independent columns, it must have a column space (and hence row space) of dimension , causing by the definition of rank. Hence.

Find the rank of the following matrix.

$\begin{bmatrix} 10 & 2 \ 4 & 5\ 5& 10 \end{bmatrix}$

Explanation

We need to get the matrix into reduced echelon form, and then count all the non all zero rows.

$R_2-\frac{2}{5}R_1\rightarrow R_2$

$\begin{bmatrix} 10 & 2 \ 0 & \frac{21}{5}\ 5& 10 \end{bmatrix}$

$R_3-\frac{1}{2}R_1\rightarrow R_3$

$\begin{bmatrix} 10 & 2 \ 0 & \frac{21}{5}\ 0& 9 \end{bmatrix}$

$R_2 \leftrightarrow R_3$

$\begin{bmatrix} 10 & 2 \ 0& 9 \ 0 & \frac{21}{5}\end{bmatrix}$

$R_3-\frac{7}{15}R_2\rightarrow R_3$

$\begin{bmatrix} 10 & 2 \ 0& 9 \ 0 & 0\end{bmatrix}$

$\frac{1}{9}R_2\rightarrow R_2$

$\begin{bmatrix} 10 & 2 \ 0& 1 \ 0 & 0\end{bmatrix}$

$R_1-2R_2\rightarrow R_1$

$\begin{bmatrix} 10 & 0 \ 0& 1 \ 0 & 0\end{bmatrix}$

$\frac{1}{10}R_1\rightarrow R_1$

$\begin{bmatrix} 1 & 0 \ 0& 1 \ 0 & 0\end{bmatrix}$

The rank is 2, since there are 2 non all zero rows.

$\begin{align*}&\text{Determine the trace of the matrix}\&A=\begin{bmatrix}-8&-7\-3&0\end{bmatrix}\end{align*}$

Explanation

$\begin{align*}&\text{We can find the trace of a square nxn matrix by summing its diagonal elements:}\&\sum_{i=1}^{n}A_{i,i}\&\text{i.e. }Tr\begin{bmatrix}a&b&c\d&e&f\g&h&i\end{bmatrix}=a+e+i\&\text{For }A=\begin{bmatrix}-8&-7\-3&0\end{bmatrix}\&(-8)+(0)=-8\end{align*}$

True or false: A matrix with five rows and four columns has as its inverse a matrix with four rows and five columns.

False

True

Explanation

Only a square matrix - a matrix with an equal number of rows and columns - has an inverse. Therefore, a matrix with five rows and four columns cannot even have an inverse.

Let be a five-by-five matrix.

Cofactor $C_{14}$ must be equal to:

The additive inverse of Minor $M_{14}$

Minor $M_{14}$

The additive inverse of the reciprocal of Minor $M_{14}$

The reciprocal of Minor $M_{14}$

None of the other choices gives a correct response.

Explanation

$C_{mn}= ( -1 )^{m+n} M_{mn}$

Set ; the formula becomes

$C_{14}= ( -1 )^{1+4} M_{14}$

$C_{14}= ( -1 )^{5} M_{14}$

$C_{14}=-1 \cdot M_{14}$

$C_{14}=- M_{14}$ .

Therefore, the cofactor $C_{14}$ must be equal to the opposite of the minor $M_{14}$ .

Consider the matrix

$A = \begin{bmatrix} 2& 3& -1\ -2& 1& 0\ 0& 1& 2 \end{bmatrix}$

Calculate the cofactor $C_{2,1}$ of this matrix.

$C_{2,1} = -7$

$C_{2,1} = 7$

$C_{2,1} = -5$

$C_{2,1} =5$

$C_{2,1} =0$

Explanation

The cofactor $C_{m, n}$ of a matrix , by definition, is equal to

$C_{m, n} = (-1)^{m + n} M_{m, n}$ ,

where $M_{m, n}$ is the minor of the matrix - the determinant of the matrix formed when Row and Column of are struck out. Therefore, we first find the minor $M_{2,1}$ of the matrix by striking out Row 2 and Column 1 of , as shown in the diagram below: