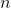Matrix-Matrix Product
Help Questions
Linear Algebra › Matrix-Matrix Product
Let 

Find 

Explanation
First, it must be established that 





Matrices are multiplied by multiplying each row of the first matrix by each column of the second - that is, by adding the products of the entries in corresponding positions. Thus,

Let 

Find 

Explanation
First, it must be established that 





Matrices are multiplied by multiplying each row of the first matrix by each column of the second - that is, by adding the products of the entries in corresponding positions. Thus,
What is dimension criteria to multiply two matrices 








Explanation
If 







True or false: A matrix whose determinant is neither 0 nor 1 cannot be an idempotent matrix.
True
False
Explanation


and, since 

By transitivity,

The only two numbers equal to their own squares are 0 and 1, so


This makes the statement true.
For any given value 

One
Zero
Two
Infinitely many
Explanation



Premultiplying both sides of the equation by 

where 

Matrix multiplication is associative, so

Therefore, the only nonsingular idempotent matrix of a given dimension 
Compute 

Not Possible
Explanation
In order to be able to multiply matrices, the number of columns of the 1st matrix must equal the number of rows in the second matrix. Here, the first matrix has dimensions of (3x2). This means it has three rows and two columns. The second matrix has dimensions of (3x2), also three rows and two columns. Since 






Which of the following is defined?
Explanation






For the product of three matrices to be defined, they must be, in order, an 





























True or false:

True
False
Explanation






Your friend Hector wants to multiply two matrices 



The number of columns in matrix 

The number of rows in matrix 

The number of rows in matrix 

The number of columns in matrix 



Explanation
Whenever we multiple two matrices together we must always check first that the number of columns in the first matrix is equal to the number of rows in the second matrix. For example, consider these two matrices
The first matrix has 3 columns, and the second matrix has 3 rows. We can multiple these two matrices together in this order. However, if we switch the order around, we will not be able to multiply these two matrices.
Now the first matrix has 4 columns and the second matrix has 2 rows. We cannot multiply these two matrices in this order.
Calculate 
Explanation
This is not as daunting a task as it seems.
First, find 
Multiply rows of 

Find 
This suggests a pattern:


This can be confirmed by mathematical induction as follows:
Suppose 
Then
Setting