GMAT Quantitative Reasoning

Help Questions

GMAT Quantitative › GMAT Quantitative Reasoning

Questions 1 - 10

Rhombus_1

The above figure shows a rhombus . Give its area.

$40 \sqrt{11}$

$40\sqrt{61}$

Explanation

Construct the other diagonal of the rhombus, which, along with the first one, form a pair of mutual perpendicular bisectors.

Rhombus_1

By the Pythagorean Theorem,

$n = \sqrt{12^{2}- 10^{2}} =\sqrt{144- 100} = \sqrt{44}= \sqrt{4}\cdot \sqrt{11} = 2 \sqrt{11}$

The rhombus can be seen as the composite of four congruent right triangles, each with legs 10 and $2 \sqrt{11}$ , so the area of the rhombus is

$A = 4 \cdot \frac{1}{2}\cdot 10 \cdot 2\sqrt{11} =40 \sqrt{11}$ .

Two angles of an isosceles triangle measure $(x + 20) ^{\circ}$ and $\left ( 100-x\right )^{ \circ}$ . What are the possible values of ?

$x = 40 \textrm{ or }x = 80$

$x = 60 \textrm{ or } x = 80$

Explanation

In an isosceles triangle, at least two angles measure the same. Therefore, one of three things happens:

Case 1: The two given angles have the same measure.

$2x \div 2 =80 \div 2$

The angle measures are $60 ^{\circ}, 60 ^{\circ}, 60 ^{\circ}$ , making the triangle equianglular and, subsequently, equilateral. An equilateral triangle is considered isosceles, so this is a possible scenario.

Case 2: The third angle has measure $(x + 20) ^{\circ}$ .

Then, since the sum of the angle measures is 180,

$\left (x + 20 \right ) +\left (x +20 \right )+ \left ( 100-x \right ) = 180$

as before

Case 3: The third angle has measure $\left ( 100-x\right )^{ \circ}$

$\left (x + 20 \right ) +\left (100-x \right )+ \left ( 100-x \right ) = 180$

as before.

Thus, the only possible value of is 40.

$\Delta ABC$ is a scalene triangle with perimeter 47; the length of each of its sides can be given by a prime whole number. What is the greatest possible length of its longest side?

This triangle cannot exist.

Explanation

A scalene triangle has three sides of different lengths, so we are looking for three distinct prime integers whose sum is 47.

There are ten ways to add three distinct primes to yield sum 47:

By the Triangle Inequality, the sum of the lengths of the shortest two sides must exceed that of the greatest. We can therefore eliminate all but four:

The greatest possible length of the longest side is 23.

Triangle

Note: Figure NOT drawn to scale.

Refer to the above diagram. Give the area of Quadrilateral .

The correct answer is not among the other choices.

Explanation

Apply the Pythagorean Theorem twice here.

$BD = \sqrt{6^{2}+ 8^{2}} = \sqrt{36+64 } = \sqrt{100}= 10$

$BC = \sqrt{26^{2}-10^{2}} = \sqrt{676-100} = \sqrt{576} = 24$

The quadrilateral is a composite of two right triangles, each of whose area is half the product of its legs:

Area of $\Delta ABD$ : $\frac{1}{2} \times 6 \times 8 = 24$

Area of $\Delta BCD$ : $\frac{1}{2} \times 10 \times 24= 120$

Add:

The arc $\widehat{AB}$ of a circle measures $90^{\circ }$ and has length . Give the length of the chord $\overline{AB}$ .

$\frac{2 \sqrt{2}}{\pi}x + \frac{4 \sqrt{2}}{\pi}$

$\frac{ \sqrt{2}}{\pi}x + \frac{ \sqrt{2}}{\pi}$

$\frac{ \pi \sqrt{2}}{4} x + \frac{ \pi \sqrt{2}}{2}$

$\frac{ \pi \sqrt{2}}{2} x + \pi \sqrt{2}$

$\pi x \sqrt{2}+ 2 \pi \sqrt{2}$

Explanation

The figure referenced is below.

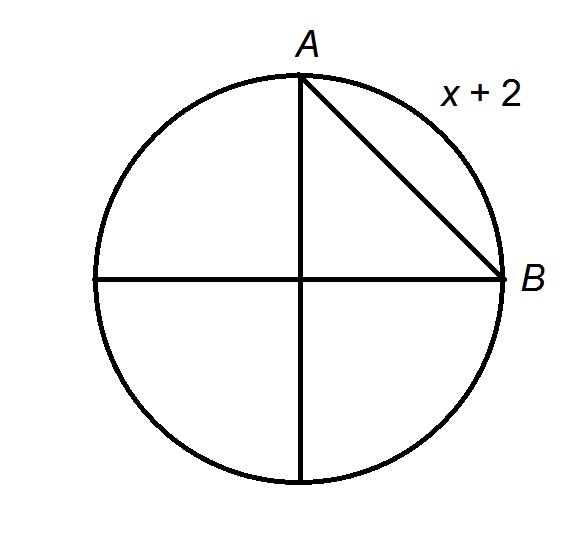
Circle x

The arc is $\frac{90}{360} = \frac{1}{4}$ of the circle, so the circumference of the circle is

The radius is this circumference divided by $2 \pi$ , or

$\frac{ 4x+8}{2 \pi} = \frac{2}{\pi}x + \frac{4}{\pi}$ .

$\overline{AB}$ is, consequently, the hypotenuse of an isosceles right triangle with leg length $\frac{2}{\pi}x + \frac{4}{\pi}$ ; by the 45-45-90 Triangle Theorem, its length is $\sqrt{2}$ times this, or

$\left (\frac{2}{\pi}x + \frac{4}{\pi} \right ) \sqrt{2} = \frac{2 \sqrt{2}}{\pi}x + \frac{4 \sqrt{2}}{\pi}$

Find the volume of a cylinder whose height is and radius is .

$32\pi$

$16\pi$

$\24\pi$

$8\pi$

Explanation

To find the volume of a cylinder, you must use the following equation:

$V=\pi{r^2}h$

Thus,

$V=\pi(2^2)(8)=32\pi$

The average of 10, 25, and 70 is 10 more than the average of 15, 30, and x. What is the missing number?

$30$

$25$

$15$

$20$

$35$

Explanation

The average of 10, 25, and 70 is 35: $\frac{10+25+70}{3}=35$

So the average of 15, 30, and the unknown number is 25 or, 10 less than the average of 10, 25, and 70 (= 35)

so $\frac{15+30+x}{3}=25$

$15+30+x=75$

$45+x=75$

$x=30$

In the -plane, point $(a,b)$ lies on a circle with center at the origin. The radius of the circle is 5. What is the value of $a^{2}+b^{2}$ ?

$25$

$5$

$10$

$16$

$32$

Explanation

$a$ and $b$ are the right-angle sides of a triangle, and the radius of the circle is the hypotenuse of the triangle. From the Pythagorean Theorem we would know that $a^{2}+b^{2}=r^{2}=5^{2}=25$ .

What is the domain of $y = 4 - x^{2}$ ?

all real numbers

$x \leq 4$

$x \geq 4$

$x \leq 0$

Explanation

The domain of the function specifies the values that can take. Here, $4-x^{2}$ is defined for every value of , so the domain is all real numbers.

Sector

The circle in the above diagram has center . Give the area of the shaded sector.

Statement 1: The circle has circumference $40 \pi$ .

Statement 2: $m \angle ACB = 30 ^{\circ }$

BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.

Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.

BOTH statements TOGETHER are insufficient to answer the question.

EITHER statement ALONE is sufficient to answer the question.

Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.

Explanation

To find the area of a sector of a circle, we need a way to find the area of the circle and a way to find the central angle of the sector.

Statement 1 alone gives us the circumference; this can be divided by $2 \pi$ to yield the radius, and that can be substituted for in the formula $A = \pi r^{2}$ to find the area. However, it provides no clue that might yield $m \angle AOB$ .

Statement 2 alone asserts that $m \angle ACB = 30 ^{\circ }$ . This is an inscribed angle that intercepts the arc $\widehat{AB}$ ; therefore, the arc - and the central angle that intercepts it - has twice this measure, or $60 ^{\circ }$ . Therefore, Statement 2 alone gives the central angle, but does not yield any clues about the area.

Assume both statements are true. The radius is $40 \pi \div 2 \pi = 20$ and the area is $A = \pi \cdot 20^{2 }= 400 \pi$ . The shaded sector is $\frac{60^{\circ }}{360^{\circ }}= \frac{1}{6}$ of the circle, so the area can be calculated to be $\frac{1}{6} \times 400 \pi = \frac{200 \pi}{3}$ .

Page 1 of 100

Return to subject

AI TutorYour personal study buddy

Question of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games