How to interpret dotplots
Help Questions
AP Statistics › How to interpret dotplots
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
Scatterplot
Histogram
Bar chart
Z-score
Bell curve
Explanation
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)


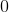





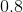
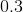


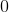


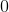
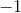

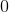


Explanation
The first graph is random scatter, no correlation, the second is perfect linear, corellation 

Yes; negative linear relationship
Yes; positive linear relationship
No; there is no correlation
Yes; negative exponential relationship
Explanation
The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
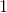
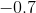




 and
and  variables? If so, describe the correlation.
variables? If so, describe the correlation.