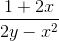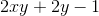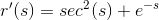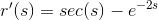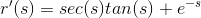Step 1: Rewrite the problem.

integral (x3+x1/2) dx from 0 to 1

Step 2: Integrate

x4/4 + 2x(2/3)/3 from 0 to 1

Step 3: Plug in bounds and solve.

\[14/4 + 2(1)(2/3)/3\] – \[04/4 + 2(0)(2/3)/3\] = (1/4) + (2/3) = (3/12) + (8/12) = 11/12

For a chain rule derivative, we need to work our way inward from the very outermost function. First, we need to do a power rule for the outer exponent. Then, we multiply that by the derivative of the inside.

To find we must use implicit differentiation, which is an application of the chain rule.

Taking of both sides of the equation, we get

using the following rules:

, ,

Note that for every derivative of a function with y, the additional term appears; this is because of the chain rule, where , so to speak, for the function it appears in.

Using algebra to rearrange, we get

We start by taking the derivative of both sides of the equation, and proceeding as follows,

.

We know how to take the derivative of , but not , so let's use the chain rule.

According to the chain rule, we should take the derivative of the outside function and multiply it by the derivative of the inside function. This gives us:

Remember that .

Our final answer:

*****************************************************************

REQUIRED KNOWLEDGE

*****************************************************************

This problem requires us to understand two things:

1. The derivative of the function is always by itself

2. By adding an operation to the variable in the exponent (in our case, the -s instead of just s), we must multiply the derivative by the derivative of the argument in the exponent. This is an application of the chain rule of derivation

*****************************************************************

SOLUTION STEPS

***************************************************************** is given

Thus:

The -1 comes from the derivative of -s

Thus, the correct answer is:

*****************************************************************

CORRECT ANSWER

*****************************************************************

*****************************************************************

PROBLEMS?

*****************************************************************

If you did not understand the concepts required to solve this derivative problem:

• Look into the derivative of e raised to an argument
• Practice applying the chain rule to derivative problems

This is a chain rule derivative. We must first start by taking the derivative of the outermost function. Here, that is a function raised to the fifth power. We need to take that derivative (using the the power rule). Then, we multiply by the derivative of the innermost function:

On this problem we have to use chain rule, which is:

So in this problem we let

and

.

Since

and

,

we can conclude that

Step 1: Rewrite the problem.

integral (x3+x1/2) dx from 0 to 1

Step 2: Integrate

x4/4 + 2x(2/3)/3 from 0 to 1

Step 3: Plug in bounds and solve.

\[14/4 + 2(1)(2/3)/3\] – \[04/4 + 2(0)(2/3)/3\] = (1/4) + (2/3) = (3/12) + (8/12) = 11/12

Use the inverse Power Rule to evaluate the integral. We know that for . But, in this case, IS equal to so a special condition of the rule applies. We must instead use . Pull the constant "3" out front and evaluate accordingly. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.