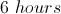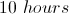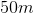Equations
Help Questions
Algebra 2 › Equations
Solve the equation:
Explanation
Add four on both sides.
To isolate the x-variable, we will need to multiply by two thirds on both sides.
The answer is:
A large tub has two faucets. The hot water faucet, if turned all the way up, can fill the tub in 16 minutes; the cold water faucet, in 12 minutes. Which of the following choices comes closest to the amount of time it takes for both faucets working together to fill the tub?
Explanation
Work problems can be solved by looking at them as rate problems.
The hot faucet can fill up the tub at a rate of 16 minutes per tub, or 

Suppose the tub fills up in 



Of the given choices, 7 minutes comes closest.
Solve the equation:
Explanation
Add 
Combine like-terms on both sides.
Subtract nine from both sides.
Divide by five on both sides.
The answer is:
Tom is painting a fence 




If Huck completes painting the entire fence after Tom leaves, how many more hours will Huck work than Tom?
Explanation
Tom paints for a total of 



to determine the total length of the fence Tom paints.

Subtracting this from the total length of the fence 




If Huck works 


A circular tower stands surrounded by a circular moat. A bridge provides a passage over the moat to the tower. The distance from the outer edge of the moat to the center of the tower is 


Explanation
The distance from the outer edge of the moat to the center of the castle is the radius (100 m) of the larger circle formed by the outer edge of the circular moat.
The radius of the tower's floor (found using the area of the floor), needs to be subracted from 100 m to find the distance fo the bridge.
Two numbers have a ratio of 5:6 and half of their sum is 22. What are the numbers?
Explanation
Set up the equation:
Solve the equation:
Find the two numbers:
The two numbers have a ratio of 5:6, therefore the ratio can also be represented as:
The two numbers are 20 and 24.
Set up the equation: Eight less than four times a number is twenty.
Explanation
Split the sentence into parts.
Four times a number:
Eight less than four times a number:
Is twenty:
Set the terms equal.
The answer is:
Set up the equation: Nine more than three times the cube of a number is four.
Explanation
Split the sentence into parts.
The cube of a number:
Three times the cube of a number:
Nine more than three times the cube of a number:
Is four:
Combine the parts to form the equation.
The answer is:
Set up the equation: Eight less than four times a number is twenty.
Explanation
Split the sentence into parts.
Four times a number:
Eight less than four times a number:
Is twenty:
Set the terms equal.
The answer is:
Set up the equation: Nine more than three times the cube of a number is four.
Explanation
Split the sentence into parts.
The cube of a number:
Three times the cube of a number:
Nine more than three times the cube of a number:
Is four:
Combine the parts to form the equation.
The answer is: