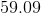Triangles
Help Questions
ACT Math › Triangles

In the figure above, 



Explanation
Assigning the length of ED the value of x, the value of AE will be 3_x_. That makes the entire side AD equal to 4_x_. Since the figure is a square, all four sides will be equal to 4_x_. Also, since the figure is a square, then angle A of triangle ABE is a right angle. That gives triangle ABE sides of 3_x_, 4_x_ and 10. Using the Pythagorean theorem:
(3_x_)2 + (4_x_)2 = 102
9_x_2 + 16_x_2 = 100
25_x_2 = 100
_x_2 = 4
x = 2
With x = 2, each side of the square is 4_x_, or 8. The area of a square is length times width. In this case, that's 8 * 8, which is 64.
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
2√5
11
10√2
15
6√2
Explanation
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Find the perimeter of an equilateral triangle given side length of 2.
Explanation
To solve, simply multiply the side length by 3 since they are all equal. Thus,
Find the perimeter of an equilateral triangle whose side length is 
Explanation
To solve, simply multiply the side length by 
What is the hypotenuse of a right triangle with side lengths 

Explanation
The Pythagorean Theorem states that . This question gives us the values of



Take 



Now we can start solving for 
The length of the hypotenuse is 

What is the value of 
Cannot be calculated
Explanation
Begin by filling in the missing angle for your triangle. Since a triangle has a total of 
Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:
Solving for 
Rounding, this is 
Find the perimeter of an equilateral triangle whose side length is 
Explanation
To solve, simply multiply the side length by 
Find the perimeter of an equilateral triangle given side length of 2.
Explanation
To solve, simply multiply the side length by 3 since they are all equal. Thus,
What is the area of a triangle with a circle inscribed inside of it, in terms of the circle's radius R?

Explanation
Draw out 3 radii and 3 lines to the corners of each triangle, creating 6 30-60-90 triangles.
See that these 30-60-90 triangles can be used to find side length.
Formula for side of equilateral triangle is

Now substitute the new equation that is in terms of R in for S.
What is the area of a triangle with a circle inscribed inside of it, in terms of the circle's radius R?

Explanation
Draw out 3 radii and 3 lines to the corners of each triangle, creating 6 30-60-90 triangles.
See that these 30-60-90 triangles can be used to find side length.
Formula for side of equilateral triangle is

Now substitute the new equation that is in terms of R in for S.