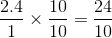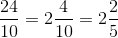Operations
Help Questions
TACHS Math › Operations
What is the difference between 

Explanation
Since the question asks you to find the difference, you will need to subtract the two fractions:
Start by making both denominators the same. Multiply the numerator and denominator of 


Now, subtract.
Make sure to simplify the answer.
What is the difference between 

Explanation
Since the question asks you to find the difference, you will need to subtract the two fractions:
Start by making both denominators the same. Multiply the numerator and denominator of 


Now, subtract.
Make sure to simplify the answer.
Which of the following is the most reduced form of 
Explanation
Start by converting 
We multiply both numerator and denominator by 
Now, convert 
Which of the following is the most reduced form of 
Explanation
Start by converting 
We multiply both numerator and denominator by 
Now, convert 
Rachel earns 


Cannot be determined
Explanation
Start by figuring out how much Rachel can earn in each week by multiplying her hourly rate by the number of hours worked each week.
Now, divide the amount she needs to earn by the amount earned each week to find how many weeks she will need to work to earn that amount.
Rachel must work for 
Rachel earns 


Cannot be determined
Explanation
Start by figuring out how much Rachel can earn in each week by multiplying her hourly rate by the number of hours worked each week.
Now, divide the amount she needs to earn by the amount earned each week to find how many weeks she will need to work to earn that amount.
Rachel must work for 
Janice's car can travel 


Explanation
Start by finding out how many gallons is currently in Janice's tank.
Since it is only 

The tank only has 
Janice's car can travel 


Explanation
Start by finding out how many gallons is currently in Janice's tank.
Since it is only 

The tank only has 
What is the product of 

Explanation
Since the question asks for the product, you will need to multiply the two fractions. Recall that in multiplying two fractions, you will multiply the numerators together and then multiply the denominators together.
Next, reduce the fraction.
What is the product of 

Explanation
Since the question asks for the product, you will need to multiply the two fractions. Recall that in multiplying two fractions, you will multiply the numerators together and then multiply the denominators together.
Next, reduce the fraction.