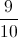How to find the probability of an outcome
Help Questions
SSAT Upper Level Quantitative › How to find the probability of an outcome
In a jar, there are 3 blue marbles, 5 red marbles, 8 green marbles. If Bob reaches his hand in a jar, and grabs one marble, what is the likelihood he will pick up a blue marble?
Explanation
First, calculate the total number of marbles in the jar, which is 

Presented with a deck of fifty-two cards (no jokers), what is the probability of drawing either a face card or a spade?
Explanation
A face card constitutes a Jack, Queen, or King, and there are twelve in a deck, so the probability of drawing a face card is 
There are thirteen spades in the deck, so the probability of drawing a spade is 
Keep in mind that there are also three cards that fit into both categories: the Jack, Queen, and King of Spades; the probability of drawing one is
Thus the probability of drawing a face card or a spade is:
Set A:
Set B:
One letter is picked from Set A and Set B. What is the probability of picking two consonants?
Explanation
Set A:
Set B:
In Set A, there are five consonants out of a total of seven letters, so the probability of drawing a consonant from Set A is 
In Set B, there are three consonants out of a total of six letters, so the probability of drawing a consonant from Set B is 
The question asks for the probability of drawing two consonants, meaning the probability of drawing a constant from Set A and Set B, so probability of the intersection of the two events is the product of the two probabilities:
Jeff collects basketball cards of players on his three favorite teams. He decides to put 5 cards from each team in a paper bag and then to draw out 3 cards at random. What are the odds of him getting one player from each team?
27.5%
6.6%
19.8%
33%
50%
Explanation
For this problem, we will multiply together the odds of each draw (assuming he draws one card at a time...the odds won't change if he draws three at once, but it's easier to visualize this way) resulting in a card that works for Jeff's goal of having one player from each team. The first draw cannot fail, as he needs one player from each team and the first card he draws must be from one of the teams. After this draw, he has 14 cards remaining, and 10 of these are players on the two teams that can still offer a player.
So the odds of a successful second draw are 
The last draw is the trickiest, as there would now be 13 cards remaining, with only 5 being players from the team that he still needs represented. When we multiply all of these odds together, we get
which is 27.5%.
A standard deck of 53 cards (including the joker) is altered by adding the sevens from another deck. What are the odds against a randomly drawn card being a heart?
Explanation
Adding the four sevens from another deck to a 53-card deck will yield a 57-card deck with 14 hearts - the original 13 hearts and the added seven of hearts - and 43 other cards. Therefore, the odds against drawing a heart will be 43 to 14.
A fair coin is tossed nine times. Each toss comes up heads. What is the probability that the coin will come up heads a tenth time?
Explanation
Each flip of the coin is an independent event, and does not affect the other flips; all that matters is that the coin is fair. Because of that fact, the probability that the tenth flip comes up heads is 
Set A:
Set B:
One letter is drawn from Set A, and one from Set B. What is the probability of drawing a matching pair of letters?
Explanation
Set A:
Set B:
Between Set A and Set B, there are two potential matching pairs of letters: AA and XX. The amount of possible combinations is the number of values in Set A, multiplied by the number of values in Set B, 
Therefore, the probability of drawing a matching set is:
A standard deck of 52 cards is altered by adding the jacks from another deck. What are the odds against a randomly drawn card being a club?
Explanation
Before the addition of the jacks, the deck had 13 clubs and 39 other cards. The 4 jacks from the other deck include 1 club and 3 other cards, so the altered deck contains 14 jacks and 42 other cards. That makes the odds against drawing a club at random

Sharon participates in a charity fundraiser in which she pays $2 to draw a card from a deck of cards; the deck is a standard 52-card deck plus the joker. If she draws the joker, she wins $25; if she draws the ace of spades, she wins $10; if she draws any other ace, she wins $7; if she draws any other card, she does not win. To the nearest cent, what is the expected value of the game to Sharon?
Explanation
Since there is only one card out of 53 (joker) that wins Sharon the $25 prize, the probability of this happening is 
Since there is only one card out of 53 (ace of spades) that wins Sharon the $10 prize, the probability of this happening is 
Since there are three cards out of 53 (ace of clubs, ace of diamonds, ace of hearts) that win Sharon a $7 prize, the probability of this happening is 
Since there are 48 out of 53 cards that do not win Sharon a prize, the probability of this happening is 

To find an expected value of a game, multiply the probability of each outcome by its value, then add the products. The expected value of this game to Sharon is therefore

The expected value of the game to Sharon rounds to 

Above is a part of the board for a popular board game. Terry is moving clockwise on the board; his playing piece is represented by the black triangle. He is about to roll a pair of fair six-sided dice. He collects $10,000 every time he lands on or passes the space marked "Onward!"
What are the odds in favor of, or against, him collecting $10,000 on this turn?
11 to 1 in favor
5 to 1 in favor
5 to 1 against
11 to 1 against
Explanation
Terry will collect $10,000 if he rolls a four or higher. As can be seen in the diagram below, out of thirty-six equally probable outcomes possible with the roll of two fair six-sided dice, there are only three rolls unfavorable to this outcome, and thirty-three favorable:

This makes the odds