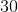Area of Polygons
Help Questions
SSAT Upper Level Quantitative › Area of Polygons
Find the area of a regular pentagon that has a side length of 

Explanation
To find the area of a regular polygon,
To find the perimeter of the pentagon,
For the given pentagon,
So then, to find the area of the pentagon,
Find the area of a regular hexagon that has side lengths of 
Explanation
Use the following formula to find the area of a regular hexagon:

Now, substitute in the length of the side into this equation.
The area of a rectangle is 

Explanation
Let 


Since this is the length in feet, we multiply this by 12 to get the length in inches:
A rectangle has the area of 80 square inches. The width of the rectangle is 2 inches longer that its height. Give the height of the rectangle.
Explanation
The area of a rectangle is given by multiplying the width times the height. That means:
where:


We know that: 

Now we should solve the equation for 
The equation has two answers, one positive 


Find the area of a regular pentagon that has a side length of 

Explanation
To find the area of a regular polygon,
To find the perimeter of the pentagon,
For the given pentagon,
So then, to find the area of the pentagon,
A rectangle has the area of 80 square inches. The width of the rectangle is 2 inches longer that its height. Give the height of the rectangle.
Explanation
The area of a rectangle is given by multiplying the width times the height. That means:
where:


We know that: 

Now we should solve the equation for 
The equation has two answers, one positive 


The area of a rectangle is 

Explanation
Let 


Since this is the length in feet, we multiply this by 12 to get the length in inches:
Find the area of a regular hexagon that has side lengths of 
Explanation
Use the following formula to find the area of a regular hexagon:

Now, substitute in the length of the side into this equation.

Figure NOT drawn to scale.
The above depicts Rhombus 

Give the area of Rhombus 
Explanation
The area of any parallelogram is the product of the length of its base and that of a corresponding altitude. We can take 

All four sides of a rhombus have the same length, so we can find 
Now multiply the lengths of this base and the altitude to get the area:

Figure NOT drawn to scale
The above figure shows Rhombus 



Give the area of Rectangle 
Explanation
A rhombus, by definition, has four sides of equal length. Therefore, 






Also, both 


The figure, with the lengths, is below.

The area of the entire Rhombus 



Rectangle 




From the Division Property, it follows that

and

This makes 450 the area of Rectangle