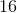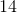How to find a triangle on a coordinate plane
Help Questions
SSAT Middle Level Quantitative › How to find a triangle on a coordinate plane
The above triangle has base 6 and height 4. Find the perimeter.
Explanation
Because the y-axis bisects the base, we can divide the triangle into two, equal right triangles. The base of the right triangle is thus half that of the larger triangle, or 3. The height is still 4. To find the hypotenuse, use the Pythagorean Theorem:
Thus, we now know the base as given in the problem and each of the other two sides (which are also the hypotenuses of the right triangles).
Therefore, the perimeter is:
Find the area of the above triangle, given that it has a height of 12 and a base of 10.
Explanation
Because this is a right triangle, the area formula is simply:
Thus, the solution is:
Given triangle 


Explanation
Use the Pythagorean Theorem to find the length of side AC:
Then, the perimeter is simply the sum of all three sides:
The isosceles triangle shown above has a perimeter of 22 and base of 6. Find the lengths of the left and right sides, respectively. Assume no other side has a length of 6.
Explanation
With a perimeter of 22 and base of 6, this means the other two sides must add up to:
Because an isosceles triangle must have two sides equal in length and we know from the problem that no other side equals 6, the two remaining sides must be equal to each other.
Thus, to be equal to each other and also add up to 16, each side must be 8 units in length.
Given triangle 




Explanation
To find the area of this triangle, we first need to determine the length of sides AB and BC. First, point B shares the same x-coordinate as point A and the same y-coordinate as point C. Thus, B must be located at point (-2,-2).
The length of side AB must then be:
and the length of side BC:
Using the area formula,
we can find the area using the base (side BC) and height (side AB):
Given the above triangle is an equilateral triangle, find the perimeter in units as drawn in the coordinate system.
Explanation
Using the coordinate system, one can see the base of the triangle is 6 units in length. Since it is an equilateral triangle, the other two sides must also be 6 units each in length. Therefore the perimeter is:
Given a height of 

Explanation
The area of any triangle is calculated by the formula:
Thus, the area of this triangle is:
Given the above triangle has a base of 

Explanation
Use the Pythagorean Theorem,
where 


Rearranging to solve for the height, 
Given the above triangle has a base of 5 and height of 6, what is the perimeter of the triangle?
Explanation
First, use the Pythagorean Theorem to find the length of the hypotenuse:




Thus,
Finally, the perimeter is the sum of the sides of the triangle or: