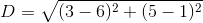Area of a triangle can be determined using the equation:

For the sake of simplicity, we will assume that the second square has sidelength 1; Then its perimeter is , and its area is .

The perimeter of the first square is , and its sidelength is . The area of this square is therefore .

The ratio of the areas is therefore .

Each side can be divided into three 3-foot sections. This gives a total of squares. Another way of looking at the problem is that the total area of the large square is 81 and each smaller square has an area of 9. Dividing 81 by 9 gives the correct answer.

A square that has an area of 81 has sides that are the square root of 81 (side2 = area for a square). Thus each of the four sides is 9. The sum of three of these sides is .

The perimeter of a shape is the length around the shape. In order to find the perimeter of a triangle, add the lengths of the sides: .

Because the lengths are in inches, the answer must be in inches as well.

Area of a triangle can be determined using the equation:

Since 1 yard = 3 feet, multiply each dimension by 3 to convert from yards to feet:

Use the area formula, substituting :

square feet

Each side can be divided into three 3-foot sections. This gives a total of squares. Another way of looking at the problem is that the total area of the large square is 81 and each smaller square has an area of 9. Dividing 81 by 9 gives the correct answer.

In geometry, a right angle triangle can occur with the ratio of in which 3 and 4 are each leg lengths, and 5 is the hypotenuse.

When you know the length of two sides of a right angle triangle like this, you can calculate the third side using this ratio.

Here, the ratio is:

This is double the ratio. Therefore, we should multiply 4 by 2 in order to solve for the missing leg, which would be a value of 8 feet.

Another way to solve is to use the Pythagorean Theorem: .

We know that one leg is 6 feet and the hypotenuse is 10 feet.

The length of a line segment can be determined using the distance formula: