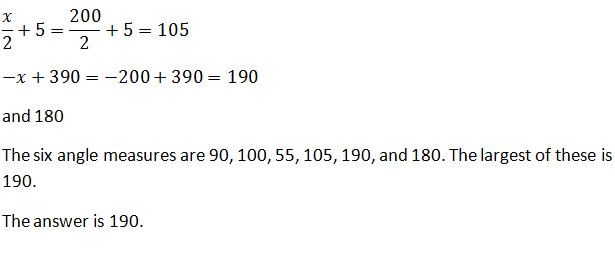Hexagons
Help Questions
SAT Math › Hexagons

The provided image represents a track in the shape of a regular hexagon with perimeter one fourth of a mile.
Teresa starts at Point A and runs clockwise until she gets halfway between Point E and Point F. How far does she run, in feet?
Explanation
One mile is equal to 5,280 feet; one fourth of a mile is equal to
Each of the six congruent sides measures one sixth of this, or
Teresa runs clockwise from Point A to halfway between Point E and Point F, so she runs along four and one half sides, for a total of

The provided image represents a track in the shape of a regular hexagon with perimeter one fourth of a mile.
Teresa starts at Point A and runs clockwise until she gets halfway between Point E and Point F. How far does she run, in feet?
Explanation
One mile is equal to 5,280 feet; one fourth of a mile is equal to
Each of the six congruent sides measures one sixth of this, or
Teresa runs clockwise from Point A to halfway between Point E and Point F, so she runs along four and one half sides, for a total of
Find the sum of all the inner angles in a hexagon.
Explanation
To solve, simply use the formula to find the total degrees inside a polygon, where n is the number of vertices.
In this particular case, a hexagon means a shape with six sides and thus six vertices.
Thus,
Find the sum of all the inner angles in a hexagon.
Explanation
To solve, simply use the formula to find the total degrees inside a polygon, where n is the number of vertices.
In this particular case, a hexagon means a shape with six sides and thus six vertices.
Thus,
An equilateral triangle with side length 
Explanation
Because it can be split into two 
With that in mind, the equilateral triangle in question has area of 
Now consider that a regular hexagon can be split into six congruent equilateral triangles with a vertex at the center and the side opposite the center as one of the hexagon's sides (a handy way of finding a hexagon's area if you can't use the regular polygon formula requiring an apothem.) Knowing that, our answer is 
An equilateral triangle with side length 
Explanation
Because it can be split into two 
With that in mind, the equilateral triangle in question has area of 
Now consider that a regular hexagon can be split into six congruent equilateral triangles with a vertex at the center and the side opposite the center as one of the hexagon's sides (a handy way of finding a hexagon's area if you can't use the regular polygon formula requiring an apothem.) Knowing that, our answer is 
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
Explanation
The sum of the interior angles of a polygon is given by 

If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
Explanation
The sum of the interior angles of a polygon is given by