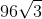How to simplify square roots
Help Questions
SAT Math › How to simplify square roots
Simplfy the following radical 
Explanation
You can rewrite the equation as 
This simplifies to 
what is
√0.0000490
49
7
0.00007
0.007
0.07
Explanation
easiest way to simplify: turn into scientific notation
√0.0000490= √4.9 X 10-5
finding the square root of an even exponent is easy, and 49 is a perfect square, so we can write out an improper scientific notation:
√4.9 X 10-5 = √49 X 10-6
√49 = 7; √10-6 = 10-3 this is equivalent to raising 10-6 to the 1/2 power, in which case all that needs to be done is multiply the two exponents: 7 X 10-3= 0.007
Simplify:
Explanation
To simplify radicals, we need to find a perfect square to factor out. In this case, its 
Which of the following is equal to 
Explanation
√75 can be broken down to √25 * √3. Which simplifies to 5√3.
What is 
Explanation
We know that 25 is a factor of 50. The square root of 25 is 5. That leaves 
Simplify:
Explanation
4√27 + 16√75 +3√12 =
4*(√3)*(√9) + 16*(√3)*(√25) +3*(√3)*(√4) =
4*(√3)*(3) + 16*(√3)*(5) + 3*(√3)*(2) =
12√3 + 80√3 +6√3= 98√3
Simplify:
Explanation
To simplify radicals, we need to find a perfect square to factor out. In this case, its 
Simplify
9 ÷ √3
3√3
3
2
not possible
none of these
Explanation
in order to simplify a square root on the bottom, multiply top and bottom by the root

Simplify:
It's impossible because the value is negative.
Explanation
Although the exponent is negative, we know that 

Simplify the following:
Explanation
To solve, you must first break up 54 into its smallest prime factors. Those are:
Since our root has index 2, that means that for every 2 identical factors inside, you can pull 1 out. Thus, we get