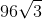You can rewrite the equation as .

This simplifies to .

easiest way to simplify: turn into scientific notation

√0.0000490= √4.9 X 10-5

finding the square root of an even exponent is easy, and 49 is a perfect square, so we can write out an improper scientific notation:

√4.9 X 10-5 = √49 X 10-6

√49 = 7; √10-6 = 10-3 this is equivalent to raising 10-6 to the 1/2 power, in which case all that needs to be done is multiply the two exponents: 7 X 10-3= 0.007

To simplify radicals, we need to find a perfect square to factor out. In this case, its .

√75 can be broken down to √25 * √3. Which simplifies to 5√3.

We know that 25 is a factor of 50. The square root of 25 is 5. That leaves which can not be simplified further.

4√27 + 16√75 +3√12 =

4*(√3)*(√9) + 16*(√3)*(√25) +3*(√3)*(√4) =

4*(√3)*(3) + 16*(√3)*(5) + 3*(√3)*(2) =

12√3 + 80√3 +6√3= 98√3

To simplify radicals, we need to find a perfect square to factor out. In this case, its .

in order to simplify a square root on the bottom, multiply top and bottom by the root

Although the exponent is negative, we know that . Therefore, we have . Let's simplify this by finding perfect squares.

To solve, you must first break up 54 into its smallest prime factors. Those are:

Since our root has index 2, that means that for every 2 identical factors inside, you can pull 1 out. Thus, we get