How to find the domain of a function
Help Questions
SAT Math › How to find the domain of a function
Which of the following functions has a domain that includes all real values of 
Explanation
The domain of a function includes all of the values of x for which that function is defined. In other words, the domain is all of the real values of x that will produce a real number. Let's look at the domains of each function one at a time.
First, let's examine
In general, when we are examining the domain of a function, we want to find places where we end up with zeros in the denominators or square-roots of negative numbers. For example, in the function 
Next, let's look at 
Subtract one from both sides.
Take the cube root of both sides.
Thus, if x = –1, then f(x) will be equal to 1/0, which isn't defined, because we can't divide by zero. Therefore, we can eliminate this answer choice.
Now, let's analyze 
We can never take the square root of a negative number. Thus, if 

Next, let's look at 
![a^{\frac{b}{c}}=\sqrt[c]{a^b}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/17894/gif.latex)


By process of elimination the answer must be 
The answer is
Let 
If 


Explanation
Because x and y must be negative integers greater than negative five, then x and y can only be equal to the following values:
x can equal -4, -3, -2, or -1
y can equal -4, -3, -2, or -1
Now we can try all of the combinations of x and y, and see what x # y would equal. It is helpful to note that x # y is the same as y # x because 2yx + y + x = 2xy + x + y. This means that the order of x and y doesn't matter.
-4 # -4 = 2(-4)(-4) + -4 + -4 = 24
-4 # -3 = 2(-4)(-3) + -4 + -3 = 17
-4 # -2 = 10
-4 # -1 = 3
-3 # -3 = 12
-3 # -2 = 7
-3 # -1 = 2
-2 # -2 = 4
-2 # -1 = 1
-1 # -1 = 0
We don't need to find -3 # -4, -2 # -4, etc, because x # y = y # x .
The smallest value of x # y must be 0.
What is the domain of the function f(x) = 2/(7x – 1) ?
x > (1/7)
x < (1/7)
x < (–1/7)
x > (–1/7)
x ≠ (1/7)
Explanation
The domain means what real number can you plug in that would still make the function work. For this case, we have to worry about the denominator so that it does not equal 0, so we solve the following. 7x – 1 = 0, 7x = 1, x = 1/7, so when x ≠ 1/7 the function will work.
Find the domain of the function:
All real numbers except for 1
All real numbers
All real numbers except for –2
0
Explanation
If a value of x makes the denominator of a equation zero, that value is not part of the domain. This is true, even here where the denominator can be "cancelled" by factoring the numerator into
and then cancelling the 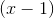
This new expression, 



Thus the domain of the function is all 
What is the domain of the given function?
x ≠ –3
All real numbers
x ≠ 3, –3
x ≠ 3
x ≠ 0
Explanation
The domain of the function is all real numbers except x = –3. When x = –3, f(–3) is undefined.
x = 0
x = 1
x = 1.5
x = 2
x = 3
Explanation
Let 

I. 1
II. 2
III. –1
I only
II only
III only
I and II
I, II, and III
Explanation
The domain of f(x) is defined as all of the values of x for which f(x) is defined.
The first value we have to consider is 1. Let's find f(1):
f(1) = (13 – 3(1)2 +2(1))–1
= (1 – 3(1) + 2)–1
= (1 – 3 + 2)–1
= (0)–1.
Remember that, in general, a–1 = 1/a. Thus, 0–1 = 1/0. However, it is impossible to have 0 in the denominator of a fraction, because it is impossible to divide anything by zero. Thus, 0–1 is undefined. Since f(1) is undefined, 1 cannot belong to the domain of f(x).
Now let's find f(2):
f(2) = (23 – 3(2)2 +2(2))–1
= (8 – 3(4) + 4)–1
=(8 – 12 + 4)–1
= 0–1
Because f(2) is undefined, 2 is not in the domain of f(x).
Finally, we can look at f(–1):
f(–1) = ((–1)3 – 3(–1)2 +2(–1))–1
= (–1 – 3(1) – 2)–1
= (–1 – 3 – 2)–1 = (–6)–1 = –1/6.
f(–1) is defined, so –1 belongs to the domain of f(x).
Therefore only III is in the domain of f(x).
Which of the following represents the domain of 

Explanation
Using our properties of exponents, we could rewrite 
This means that when we input 

The first step is to subtract 2 from 

Then we must take the fifth root of a value. The trick to this problem is recognizing that we can take the fifth root of any number, positive or negative, because the function 





Find the domain of the following function.
Explanation
To find the domain, you must find all the values you can put in for x. Thus, you must figure out what values would "break" your function and give you something unable to be computed.
First we know that the number inside a square root must be positive. Thus, we can set the inside greater than or equal to 0 and solve.
We also know that the denominator of a fraction must never be 0. Thus, if we find out when it is 0, we can exclude that x value from our domain.
If we combine both of these for x, we can create an interval for our domain.
Find the domain of the given function:
All real numbers
All real numbers x such that x ≠ 1, 0
All real numbers x such that x ≠ 3, 0
All real numbers x such that x ≠ 3
All real numbers x such that x ≠ 0
Explanation
When x = 0 or x = 3, the function is undefined due to its denominator.
Thus the domain is all real numbers x, such that x is not equal to 0 or 3.


























![\sqrt[5]{(x-2)^{4}}+3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/186063/gif.latex)








