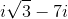Express as a power of ; that is: .

Then .

Using the properties of exponents, .

Therefore, , so .

We can use Heron's formula to find the area of the triangle. We can let a = 6, b = 10, and c = 12.

In order to find s, we need to find one half of the perimeter. The perimeter is the sum of the lengths of the sides of the triangle.

Perimeter = a + b + c = 6 + 10 + 12 = 28

In order to find s, we must multiply the perimeter by one-half, which would give us (1/2)(28), or 14.

Now that we have a, b, c, and s, we can calculate the area using Heron's formula.

Rewrite in their imaginary terms.

Use the FOIL method (first, outer, inner, last) to multiply expressions and combine like terms:

In order to solve for the x value you set both equations equal to each other (0.5x+3=3x-2). This gives you the x value for the point of intersection at x=2. Plugging x=2 into either equation gives you y=4.

We want to isolate the variable on one side and numbers on another side. Treat like a normal equation.

Subtract on both sides.

Divide on both sides.

Let = 1st even number, = 2nd even number, and = 3rd even number.

Then the equation to solve becomes .

Thus , so the middle number is 14.

In order to solve for the x value you set both equations equal to each other (0.5x+3=3x-2). This gives you the x value for the point of intersection at x=2. Plugging x=2 into either equation gives you y=4.

When multplying exponents, we need to make sure we have the same base.

Since we do, all we have to do is add the exponents.

The answer is .

You can subtract the second equation from the first equation to eliminate y:

7_x_ + y = 25 – 6_x_ + y = 23: 7_x_ – 6_x_ = x; y – y = 0; 25 – 23 = 2

x = 2

You could also solve one equation for y and substitute that value in for y in the other equation:

6_x_ + y = 23 → y = 23 – 6_x_.

7_x_ + y = 25 → 7_x_ + (23 – 6_x_) = 25 → x + 23 = 25 → x = 2