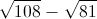Square Roots and Operations
Help Questions
PSAT Math › Square Roots and Operations
Simplify:
Explanation
To combine radicals, they must have the same radicand. Therefore, we must find the perfect squares in each of our square roots and pull them out.
Now, we plug these equivalent expressions back into our equation and simplify:
Simplify:
Explanation
To combine radicals, they must have the same radicand. Therefore, we must find the perfect squares in each of our square roots and pull them out.
Now, we plug these equivalent expressions back into our equation and simplify:
If 

Explanation
Square both sides:
x = (32)2 = 92 = 81
If 

Explanation
Square both sides:
x = (32)2 = 92 = 81
The square root(s) of 36 is/are .
6 and -6
6
-6
6, -6, and 0
None of these answers are correct.
Explanation
To square a number is to multiply that number by itself. Because 6 x 6 = 36 AND -6 x -6 = 36, both 6 and -6 are square roots of 36.
The square root(s) of 36 is/are .
6 and -6
6
-6
6, -6, and 0
None of these answers are correct.
Explanation
To square a number is to multiply that number by itself. Because 6 x 6 = 36 AND -6 x -6 = 36, both 6 and -6 are square roots of 36.
Evaluate:
None of the available answers
Explanation
Let us factor 108 and 81
Evaluate:
None of the available answers
Explanation
Let us factor 108 and 81
Simplify:
Explanation
To simplfy, we must first distribute the square root.
Next, we can simplify each of the square roots.
Simplify:
Explanation
To simplfy, we must first distribute the square root.
Next, we can simplify each of the square roots.