Find the value of the sine or cosine functions of an angle given a point on its terminal side
Help Questions
Pre-Calculus › Find the value of the sine or cosine functions of an angle given a point on its terminal side
Please choose the best answer from the following choices.
Find the secant value of 
Explanation
First, use the Pythagorean Theorem to solve for all the sides of the triangle. You know that the adjacent side is 4 units long, and the opposite side is -9 units long.
Using the Pythagorean Theorem, you should get a hypotenuse of 
Secant is defined as hypotenuse/opposite.
Thus, giving you an answer of 
What is the sine of an angle if a point on the terminal side of the angle is 
Explanation
Given the point on the coordinate plane 
The hypotenuse of the right triangle formed by the origin and the point is 
The length of the triangle is 1 unit, and the height of the triangle is 5.
Sine of an angle is opposite side divided by the hypotenuse.
Rationalize the denominator.
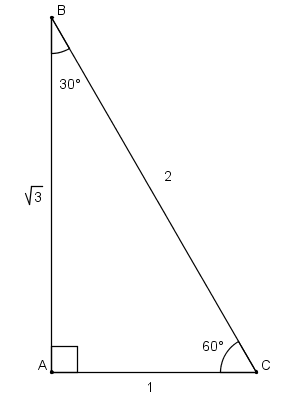
Find the sine value of 
Explanation
This is a 30-60-90 triangle. A 30-60-90 triangle will have leg lengths of 

Find the sine and cosine of the following angle.

Explanation
We see that the point on the terminal side is (5,6). So we know that with this point a right triangle is formed with a base that is 5 units long, and a leg that is 6 units high. We can use the Pythagorean Theorem to solve for the hypotenuse that is formed by this triangle and this will tell us the distance of the point from the origin.
Let’s solve for sine first. When working with right triangles recall that 
We can solve for cosine if we recall that 
The method of solving for trigonometric functions of an angle given a point on its terminal side only works for acute angles.
Which of the following statements best describes the validity of the statement above?
The statement is true
The statement is false
Explanation
Consider the figure below.
We can form a triangle by dropping a line down from the point (-2,3) perpendicular to the
x axis. Now we have right triangle that has a leg that is 3 units high and a base that is 2
units long. Now we can use the Pythagorean Theorem to solve for the hypotenuse.
We can solve for sine and cosine now. Use the fact that . The opposite side of the angle in this case is the leg that is 3 units high.
And we will use the fact that . The adjacent side to the angle is the base that is 2 units long. We do have to note that we are using
and not
.
So even though our angle was obtuse, we can still use the same method.
Find the value of the cosine of an angle given that the point on the terminal side of the angle is (3,4).
Explanation
Using the point (3,4), we can see that this forms a right triangle that has a base that is 3 units in length and an adjoining leg that is 4 units high. We are able to find the hypotenuse of this triangle using the Pythagorean Theorem. This will give us the distance of the point (3,4) to the origin.
And so the hypotenuse of this triangle (the distance from our point we are working with to the origin), is 5 units long. Recall that when using cosine for right triangles, cosine represents the following
So if we are considering the angle formed by the x-axis and our hypotenuse, the adjacent side would be the base of our triangle; 3 units.
Given that the cosine of an angle is 
If you are able to solve for the sine and cosine of an angle given a point on its terminal side, you have enough information to also solve for its tangent.
Which of the following best describes the validity of the above statement?
The statement is false in all cases.
The statement is true in all cases.
The statement is true in some cases, but not all.


















 ,
, 































 . So if
. So if




