Find the Period of a Sine or Cosine Function
Help Questions
Pre-Calculus › Find the Period of a Sine or Cosine Function
What is the period of this sine graph?

Explanation
The graph has 3 waves between 0 and 


Write the equation for a cosine graph with a minimum at 

Explanation
The equation for this graph will be in the form 
To write this equation, it is helpful to sketch a graph:
From sketching the maximum and the minimum, we can see that the graph is centered at 
The distance between the maximum and the minimum is half the wavelength. Here, it is 

The minimum occurs in the middle of the graph, so to figure out where it starts, subtract 
This graph's equation is

What is the period of this graph?

Explanation
One wave of the graph goes exactly from 0 to 

What is the period of the graph 
Explanation
The equation for this function is in the form
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
By looking at the equation, we can see that the frequency, 

The period is 

Please choose the best answer from the following choices.
Find the period of the following function in radians:
Explanation
If you look at a graph, you can see that the period (length of one wave) is 

Give the period and frequency for the equation 
Period: 
Period: 
Period: 
Period: 
Period: 
Explanation
Our equation is in the form
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
We can look at the equation and see that the frequency, 

The period is 

Please choose the best answer from the following choices.
Find the period of the following function.
Explanation
The period is defined as the length of one wave of the function. In this case, one full wave is 180 degrees or 

Given 
Explanation
The formula for the period of a sine/cosine function is 
With the standard form being:
Since 

Simplified, the period is 
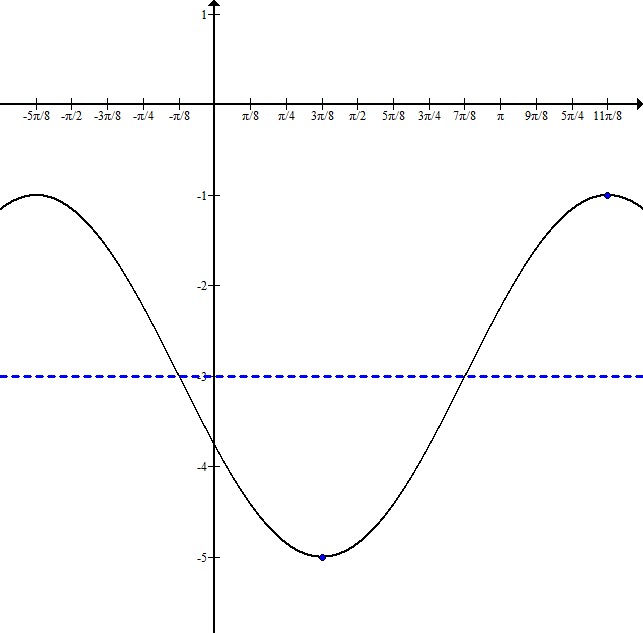
What could be the function for the following graph?
Explanation
What could be the function for the following graph?
Begin by realizing we are dealing with a periodic function, so sine and cosine are your best bet.
Next, note that the range of the function is 

From this information, we can find the amplitude:
So our function must have a 
Also, from the point 
The only remaining obstacle, is whether the function is sine or cosine. Recall that sine passes through 

Thus, our answer is:

















































