Triangles - Trigonometry
Card 0 of 644
Which of the following is true about the right triangle below?
Which of the following is true about the right triangle below?
Since the pictured triangle is a right triangle, the unlabeled angle at the lower left is a right angle measuring 90 degrees. Since interior angles in a triangle sum to 180 degrees, the unlabeled angle at the upper left can be calculated by 180 - 45 - 90 = 45. The pictured triangle is therefore a 45-45-90 triangle. In a 45-45-90 triangle, the ratio between the two short side lengths is 1:1. Therefore, A = B. Triangles with two congruent side lengths are isosceles by definition.
Since the pictured triangle is a right triangle, the unlabeled angle at the lower left is a right angle measuring 90 degrees. Since interior angles in a triangle sum to 180 degrees, the unlabeled angle at the upper left can be calculated by 180 - 45 - 90 = 45. The pictured triangle is therefore a 45-45-90 triangle. In a 45-45-90 triangle, the ratio between the two short side lengths is 1:1. Therefore, A = B. Triangles with two congruent side lengths are isosceles by definition.
Compare your answer with the correct one above
Which of the following is not a theorem to prove that triangles are similar?
Which of the following is not a theorem to prove that triangles are similar?
ASA (Angle Side Angle) is a theorem to prove triangle congruency.
In this case, we only need two angles to prove that two triangles are similar, so the last side in ASA is unnecessary for this question.
For this purpose, we use the theorem AA instead.
ASA (Angle Side Angle) is a theorem to prove triangle congruency.
In this case, we only need two angles to prove that two triangles are similar, so the last side in ASA is unnecessary for this question.
For this purpose, we use the theorem AA instead.
Compare your answer with the correct one above
What does the scale factor of a dilation need to be to ensure that triangles are not only similar but also congruent?
What does the scale factor of a dilation need to be to ensure that triangles are not only similar but also congruent?
The scale factor of a dilation tells us what we multiply corresponding sides by to get the new side lengths. In this case, we want these lengths to be the same to get congruent triangles. Thus, we must be looking for the multiplicative identity, which is 1.
The scale factor of a dilation tells us what we multiply corresponding sides by to get the new side lengths. In this case, we want these lengths to be the same to get congruent triangles. Thus, we must be looking for the multiplicative identity, which is 1.
Compare your answer with the correct one above
What is the ratio of the side opposite the 
angle to the hypotenuse?
What is the ratio of the side opposite the
Step 1: Locate the side that is opposite the 
side..
The shortest side is opposite the 
angle. Let's say that this side has length 
.
Step 2: Recall the ratio of the sides of a 
triangle:
From the shortest side, the ratio is 
.
is the hypotenuse, which is twice as big as the shortest side..
The ratio of the short side to the hypotenuse is 
Step 1: Locate the side that is opposite the
The shortest side is opposite the
Step 2: Recall the ratio of the sides of a
From the shortest side, the ratio is
The ratio of the short side to the hypotenuse is
Compare your answer with the correct one above
What is the height of an equilateral triangle with side length 8?
What is the height of an equilateral triangle with side length 8?
The altitude of an equilateral triangle splits it into two 30-60-90 triangles. The height of the triangle is the longer leg of the 30-60-90 triangle. If the hypotenuse is 8, the longer leg is 
.
To double check the answer use the Pythagorean Thereom:
The altitude of an equilateral triangle splits it into two 30-60-90 triangles. The height of the triangle is the longer leg of the 30-60-90 triangle. If the hypotenuse is 8, the longer leg is
To double check the answer use the Pythagorean Thereom:
Compare your answer with the correct one above
In a 
triangle, the side opposite the 
degree angle is 
. How long is the side opposite the 
degree angle?
In a
Based on the 30-60-90 identity, the measure of the side opposite the 30 degree angle is doubled to get the hypotenuse.
Therefore,
Based on the 30-60-90 identity, the measure of the side opposite the 30 degree angle is doubled to get the hypotenuse.
Therefore,
Compare your answer with the correct one above
In a 30-60-90 triangle, the length of the side opposite the 
angle is 
. What is the length of the hypotenuse?
In a 30-60-90 triangle, the length of the side opposite the
By definition, the length of the hypotenuse is twice the length of the side opposite the 
angle.
Recall that the hypotenuse is the side opposite the 
angle.
Thus, using the equation below, where ss represents the short side (that opposite the 
angle) we get:
Plugging in our values for the short side we find the hypotenuse as follows:
By definition, the length of the hypotenuse is twice the length of the side opposite the
Recall that the hypotenuse is the side opposite the
Thus, using the equation below, where ss represents the short side (that opposite the
Plugging in our values for the short side we find the hypotenuse as follows:
Compare your answer with the correct one above
A triangle has three angles 
, 
and 
such that 
and 
. The side opposite to 
measures 
units in length. How long is the side opposite of 
?
A triangle has three angles
A triangle with a 
angle relation is a 
, 
, 
degree triangle. The side opposite the smallest angle of a triangle is the shortest side, of length 
. The side opposite the largest angle is the longest side, measuring twice the length of the shortest side for this triangle, 
units.
Therefore, to make the above statement true 
.
A triangle with a
Therefore, to make the above statement true
Compare your answer with the correct one above
Triangle 
is equilateral with a side length of 
.
What is the height of the triangle?
Triangle
What is the height of the triangle?
An equilateral triangle has internal angles of 60°, so the sin of one of those angles is equivalent to the height of the triangle divided by the side length,
so..
An equilateral triangle has internal angles of 60°, so the sin of one of those angles is equivalent to the height of the triangle divided by the side length,
so..
Compare your answer with the correct one above
It is known that the smallest side of a 30-60-90 triangle is 5.
Find 
.
It is known that the smallest side of a 30-60-90 triangle is 5.
Find
We know that in a 30-60=90 triangle, the smallest side corresponds to the side opposite the 30 degree angle.
Additionally, we know that the hypotenuse is 2 times the value of the smallest side, so in this case, that is 10.
The formula for
, so 
or 
.
We know that in a 30-60=90 triangle, the smallest side corresponds to the side opposite the 30 degree angle.
Additionally, we know that the hypotenuse is 2 times the value of the smallest side, so in this case, that is 10.
The formula for
Compare your answer with the correct one above
It is known that for a 30-60-90 triangle,
.
Find the area of the triangle.
Note:
It is known that for a 30-60-90 triangle,
Find the area of the triangle.
Note:
First, we know that in a 30-60-90 triangle,
.
Also, the base is the smallest side times 
, so in our case it is 
.
The height is just the smallest side, 
.
Substituting these values into the formula given for area of a triangle, we obtain the answer 
.
First, we know that in a 30-60-90 triangle,
Also, the base is the smallest side times
The height is just the smallest side,
Substituting these values into the formula given for area of a triangle, we obtain the answer
Compare your answer with the correct one above
In a 
triangle, if one leg is 
. What is the measure of the hypotenuse?
In a
One option is to use the Pythagorean Theorem.
Since we have an isosceles triangle, both legs must be congruent.
Plug in to get your answer.
Or, you can remember the 45-45-90 identity, which states that the hypotenuse is 
times the leg.
One option is to use the Pythagorean Theorem.
Since we have an isosceles triangle, both legs must be congruent.
Plug in to get your answer.
Or, you can remember the 45-45-90 identity, which states that the hypotenuse is
Compare your answer with the correct one above
A triangle has three angles 
, 
, 
such that 
and 
together are as much as 
. What is the ratio of the longest side to the shortest?
A triangle has three angles
A triangle with the sum of two angles equaling the third is a 
triangle
A triangle with the sum of two angles equaling the third is a
Compare your answer with the correct one above
Find the value of 
in the triangle below.
Find the value of
The first two things to recognize regarding our tirangle are 1) it is a right triangle and 2) it is an isosceles triangle. The two congruent sides tell us that the two non-right angles are also congruent, and a little quick math tells us that they each equal 45 degrees. This means our right triangle is not just any right triangle but a 45-45-90 triangle.
This is important because the sides of every 45-45-90 triangle follow the same ratio. The two legs are obviously always congruent to each other (being isosceles), but to find the hypotenuse, we simply have to multiply the length of a leg by 
.
Given this fact we would be in good shape if we had the length of a leg and needed the hypotenuse. But we have the hypotenuse and need the leg, which we means we need to work backwards going this way, we need to divide the length of the hypotenuse by 
. Therefore,
However, general practice in mathematics doesn't allow us to leave a square root in the denominator. We solve this problem by rationalizing the denominator, which is accomplished by multiplying the numerator and the denominator by 
.
This effectively eliminates the square root in the denominator and provides our answer.
The first two things to recognize regarding our tirangle are 1) it is a right triangle and 2) it is an isosceles triangle. The two congruent sides tell us that the two non-right angles are also congruent, and a little quick math tells us that they each equal 45 degrees. This means our right triangle is not just any right triangle but a 45-45-90 triangle.
This is important because the sides of every 45-45-90 triangle follow the same ratio. The two legs are obviously always congruent to each other (being isosceles), but to find the hypotenuse, we simply have to multiply the length of a leg by
Given this fact we would be in good shape if we had the length of a leg and needed the hypotenuse. But we have the hypotenuse and need the leg, which we means we need to work backwards going this way, we need to divide the length of the hypotenuse by
However, general practice in mathematics doesn't allow us to leave a square root in the denominator. We solve this problem by rationalizing the denominator, which is accomplished by multiplying the numerator and the denominator by
This effectively eliminates the square root in the denominator and provides our answer.
Compare your answer with the correct one above
The following figure was made by beginning with a square. The midpoints of the four sides of the square were then joined to form another square. The process was repeated to form a third square and finally once more to form the fourth and smallest square in the middle, which has a side length of 
. Find the value of 
.
The following figure was made by beginning with a square. The midpoints of the four sides of the square were then joined to form another square. The process was repeated to form a third square and finally once more to form the fourth and smallest square in the middle, which has a side length of
We begin by realizing that the midpoints of the sides of our outer square divide each side in half. Furthermore, the sides of our second square connecting these midpoints form four right triangles in each corner of our largest square.
But these right triangles are special right triangles. They are 45-45-90 triangles, which means we can find the hypotenuse (and thus the side of our second square) by multiplying the length of the leg by 
. Therefore the length of a side of our second square is 
.
We now repeat the process, beginning by forming four new 45-45-90 triangles
To find the hypotenuse of each of these triangles (and thus the side length of our third square), we simply multiply by 
again.
We then repeat the process one final time, multiplying by 
again.
Our final hypotenuse and thus the side of our innermost square is 
.
We begin by realizing that the midpoints of the sides of our outer square divide each side in half. Furthermore, the sides of our second square connecting these midpoints form four right triangles in each corner of our largest square.
But these right triangles are special right triangles. They are 45-45-90 triangles, which means we can find the hypotenuse (and thus the side of our second square) by multiplying the length of the leg by
We now repeat the process, beginning by forming four new 45-45-90 triangles
To find the hypotenuse of each of these triangles (and thus the side length of our third square), we simply multiply by
We then repeat the process one final time, multiplying by
Our final hypotenuse and thus the side of our innermost square is
Compare your answer with the correct one above
Find the value of 
Find the value of
Solving this problem begins with realizing that all three of our triangles are not only right triangles but isosceles and are therefore 45-45-90 triangles. That means in each triangle to get from the length of a leg to the length of the hypotenuse, we simply multiply by 
. Therefore, the hypotenuse of our bottom triangle is
However, the hypotenuse of the bottom triangle is also the leg of the middle triangle. To find the hypotenuse of this triangle, we simply repeat the process.
However, again the hypotenuse of the middle triangle is also the leg of the upper triangle. To find 
, the hypotenuse of the upper triangle, we simply repeat the process one last time.
Solving this problem begins with realizing that all three of our triangles are not only right triangles but isosceles and are therefore 45-45-90 triangles. That means in each triangle to get from the length of a leg to the length of the hypotenuse, we simply multiply by
However, the hypotenuse of the bottom triangle is also the leg of the middle triangle. To find the hypotenuse of this triangle, we simply repeat the process.
However, again the hypotenuse of the middle triangle is also the leg of the upper triangle. To find
Compare your answer with the correct one above
In a 45-45-90 triangle, if the hypotenuse is 10, what is the perimeter of the triangle?
In a 45-45-90 triangle, if the hypotenuse is 10, what is the perimeter of the triangle?
Write the Pythagorean Theorem.
In a 45-45-90 triangle, the length of the legs are equal, which indicates that:
Rewrite the formula and substitute the known sides.
The lengths of the triangle are: 
Sum the three lengths for the perimeter.
Write the Pythagorean Theorem.
In a 45-45-90 triangle, the length of the legs are equal, which indicates that:
Rewrite the formula and substitute the known sides.
The lengths of the triangle are:
Sum the three lengths for the perimeter.
Compare your answer with the correct one above
Two buildings with flat roofs are 80 feet apart. The shorter building is 55 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 32o. How high is the taller building?
Two buildings with flat roofs are 80 feet apart. The shorter building is 55 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 32o. How high is the taller building?
To solve this problem, let's start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle.
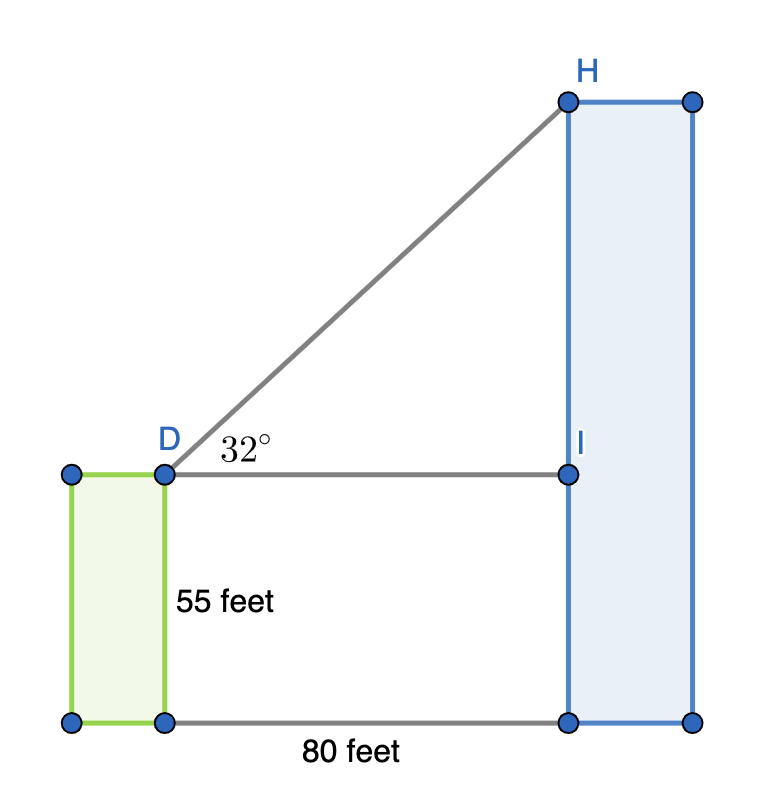
We are being asked to find the height of the taller building, but this diagram does not provide a triangle that has as one of its sides the entire height of the larger (rightmost and blue) building. However, we can instead find the distance 
, and then add that to the 40 foot height of the shorter building to find the entire height of the taller building. Start by finding 
:
Remember that this is not the full height of the larger building. To find that, we need to add 
feet. Therefore, the taller building is 104.6 feet tall.
To solve this problem, let's start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle.
We are being asked to find the height of the taller building, but this diagram does not provide a triangle that has as one of its sides the entire height of the larger (rightmost and blue) building. However, we can instead find the distance 
Remember that this is not the full height of the larger building. To find that, we need to add 
Compare your answer with the correct one above
One side of a 
-
-
triangle has a length of 3. Which cannot be the length of one of the other sides?
One side of a
If 3 is one of the legs, then the hypotenuse is 
.
If 3 is the hypotenuse, then the legs are 
or equivalently 
If 3 is one of the legs, then the hypotenuse is
If 3 is the hypotenuse, then the legs are
Compare your answer with the correct one above
The hypotenuse of a 
-
-
triangle is 4. What is the length of each of the legs?
The hypotenuse of a
Divide the length of the hypotenuse by 
to get the length of the legs:
Divide the length of the hypotenuse by
Compare your answer with the correct one above