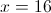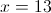SSAT Middle Level Quantitative - How to find the solution to an equation

Solve for :

Explanation

Add 45 to both sides:

James bought candy using a 10 dollar bill and received dollars in change. Which of the following describes how much James paid for the candy?

Explanation

The amount of change given after a purchase is the amount the customer pays minus the cost of the item. So the cost of the item is the amount the customer pays minus the amount of change received.

Solve for :

Explanation

$5 \cdot x+5 \cdot 7 = 80$

$5x \div 5= 45\div 5$

$(9-4) \cdot 3 = 5 + \blacksquare$ ,

then $\blacksquare$ =

Explanation

So order of operations says to do what's in the parentheses first. Thus

$5 \times 3 = 15$

Thus the left side of the equation is 15. Subtract 5 from both sides to determine what the $\blacksquare$ is.

The difference between 30 and the product of 5 and 3 is

Explanation

Order of operations says to multiply 5 and 3 first. Thus we are looking for the difference between and $\left (3\times 5\right)$ or and .

If $x\triangleright y = x- y +xy$ , then $3\triangleright 2 = ?$

Explanation

Plug in 3 where you see and 2 where you see to get $3-2+3\times2$ . This equals 7.

Call the three angles of a triangle $\angle 1, \angle 2, \angle 3$ .

The measure of $\angle2$ is forty degrees less than that of $\angle 1$ ; the measure of $\angle 3$ is ten degrees less than twice that of $\angle 1$ . If is the measure of $\angle 1$ , then which of the following equations would we need to solve in order to calculate the measures of the angles?

Explanation

The measure of $\angle2$ is forty degrees less than the measure of $\angle 1$ , so its measure is 40 subtracted from that of $\angle 1$ - that is, .

The measure of $\angle 3$ is ten degrees less than twice that of $\angle 1$ . Twice the measure of $\angle 1$ is , and ten degrees less than this is 10 subtracted from - that is, .

The sum of the measures of the three angles of a triangle is 180, so, to solve for - thereby allowing us to calulate all three angle measures - we add these three expressions and set the sum equal to 180. This yields the equation:

Call the three angles of a triangle $\angle 1, \angle 2, \angle 3$ .

The measure of $\angle2$ is twenty degrees greater than that of $\angle 1$ ; the measure of $\angle 3$ is thirty degrees less than twice that of $\angle 1$ . If is the measure of $\angle 1$ , then which of the following equations would we need to solve in order to calculate the measures of the angles?

Explanation

The measure of $\angle2$ is twenty degrees greater than the measure of $\angle 1$ , so its measure is 20 added to that of $\angle 1$ - that is, .

The measure of $\angle 3$ is thirty degrees less than twice that of $\angle 1$ . Twice the measure of $\angle 1$ is , and thirty degrees less than this is 30 subtracted from - that is, .