How to find the missing part of a list - SSAT Middle Level Quantitative
Card 1 of 132
What are the next two numbers of this sequence?

What are the next two numbers of this sequence?
Tap to reveal answer
The sequence is formed by alternately adding  and adding
and adding  to each term to get the next term.
to each term to get the next term.

 and
and  are the next two numbers.
are the next two numbers.
The sequence is formed by alternately adding 



← Didn't Know|Knew It →
Define two sets as follows:


Which of the following numbers is an element of  ?
?
Define two sets as follows:
Which of the following numbers is an element of 
Tap to reveal answer
 is the intersection of
is the intersection of  and
and  - the set of all elements appearing in both sets. Thus, an element can be eliminated from
- the set of all elements appearing in both sets. Thus, an element can be eliminated from  by demonstrating either that it is not an element of
by demonstrating either that it is not an element of  or that it is not an element of
or that it is not an element of  .
.
 is the set of positive integers ending in "5". 513 and 657 are not in
is the set of positive integers ending in "5". 513 and 657 are not in  , so they are not in
, so they are not in  .
.
 is the set of muliples of 9. We test the three remaining numbers easily by seeing if 9 divides their digit sum:
is the set of muliples of 9. We test the three remaining numbers easily by seeing if 9 divides their digit sum:



425 and 565 are not multiples of 9; neither is in  , so neither is in
, so neither is in  .
.
 and
and  , so
, so  . This is the correct choice.
. This is the correct choice.










425 and 565 are not multiples of 9; neither is in 




← Didn't Know|Knew It →
Based on the following arithmetic sequence, what is the value of  ?
?

Based on the following arithmetic sequence, what is the value of 
Tap to reveal answer
The question asks that you first determine the pattern, then use said pattern to find A and B, which can then be substituted into the equation  . The pattern is to add 5 to the previous number to achieve the next number, which results in
. The pattern is to add 5 to the previous number to achieve the next number, which results in
 and
and 
Putting A and B into the equation gives:

The other answers are wrong for the following reasons:
286 is  , not
, not 
48 is 
63 is 
624 is a result of having  , a pattern addition mistake
, a pattern addition mistake
The question asks that you first determine the pattern, then use said pattern to find A and B, which can then be substituted into the equation 

Putting A and B into the equation gives:
The other answers are wrong for the following reasons:
286 is 
48 is
63 is
624 is a result of having 
← Didn't Know|Knew It →
What is the value of  in the sequence below?
in the sequence below?

What is the value of 
Tap to reveal answer
To answer this question, the pattern must first be found. There is no common interval between the numbers, however it can be seen that the next number is the sum of the number plus the number before. A good way to address a tricky pattern is to write the difference of the two numbers above the number, as seen below where the bold numbers are the orginal numbers and the nonbolded numbers are the differences.
0 1 1 2 3
1 1 2 3 5 8
Using this pattern the value of A will be 
To answer this question, the pattern must first be found. There is no common interval between the numbers, however it can be seen that the next number is the sum of the number plus the number before. A good way to address a tricky pattern is to write the difference of the two numbers above the number, as seen below where the bold numbers are the orginal numbers and the nonbolded numbers are the differences.
0 1 1 2 3
1 1 2 3 5 8
Using this pattern the value of A will be
← Didn't Know|Knew It →
A tile layer plans to lay tile in a bathroom in the pattern shown below. What will the  tile be?
tile be?
Red, Blue, Purple, Green, Yellow, Red, Blue, Purple, Green…
A tile layer plans to lay tile in a bathroom in the pattern shown below. What will the 
Red, Blue, Purple, Green, Yellow, Red, Blue, Purple, Green…
Tap to reveal answer
The first stop to determining what the  tile will be is to determine how many repeats of the pattern will occur before hand. There are
tile will be is to determine how many repeats of the pattern will occur before hand. There are  colors in the pattern, so divide
colors in the pattern, so divide  by
by  . This results in
. This results in  with a remainder of
with a remainder of  . This means that there will be
. This means that there will be  repeats of the pattern and at the
repeats of the pattern and at the  tile, it will be at the second spot in the pattern, which is Blue. So, the
tile, it will be at the second spot in the pattern, which is Blue. So, the  tile is Blue.
tile is Blue.
The first stop to determining what the 








← Didn't Know|Knew It →
What is the value of y in the pattern below?

What is the value of y in the pattern below?
Tap to reveal answer
What that the fractions in this pattern have in common is that they are all the equivalent of  .
.
The value of y should be a number that is the equivalent of  when divided by 12.
when divided by 12.
Given that  of 12 is 4,
of 12 is 4,  of 12 would be equal to 8, the correct answer.
of 12 would be equal to 8, the correct answer.
What that the fractions in this pattern have in common is that they are all the equivalent of 
The value of y should be a number that is the equivalent of 
Given that 

← Didn't Know|Knew It →
What is the value of  in the sequence below?
in the sequence below?

What is the value of 
Tap to reveal answer
In this sequence, every subsequent number is equal to one third of the preceding number:




Given that  , that is the correct answer.
, that is the correct answer.
In this sequence, every subsequent number is equal to one third of the preceding number:
Given that 
← Didn't Know|Knew It →
Complete the set by determining the value of  .
.

Complete the set by determining the value of 
Tap to reveal answer
The set is composed of consecutive squares.


We can see that  will b equal to
will b equal to 

Therefore, 36 is the correct answer.
The set is composed of consecutive squares.
We can see that 
Therefore, 36 is the correct answer.
← Didn't Know|Knew It →
Find the next number that should appear in the set below:

Find the next number that should appear in the set below:
Tap to reveal answer
In this set, each subsequent fraction is half the size of the preceding fraction; (the denominator is doubled for each successive fraction, but the numerator stays the same). Given that the last fraction in the set is  , it follows that the subsequent fraction will be
, it follows that the subsequent fraction will be  .
.
In this set, each subsequent fraction is half the size of the preceding fraction; (the denominator is doubled for each successive fraction, but the numerator stays the same). Given that the last fraction in the set is 

← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.
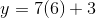
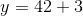

In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 
 value for . We can plug
value for . We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 



← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →
Complete the table below using the equation 

Complete the table below using the equation

Tap to reveal answer
In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding  value for
value for  . We can plug
. We can plug  into the
into the  in our equation to solve for
in our equation to solve for  .
.



In order to solve this question, we need to use both the equation and the table. We are looking for the corresponding 




← Didn't Know|Knew It →