Acute / Obtuse Triangles

Help Questions

SAT Math › Acute / Obtuse Triangles

Questions 1 - 10

Which of the following can NOT be the angles of a triangle?

45, 45, 90

1, 2, 177

30.5, 40.1, 109.4

45, 90, 100

30, 60, 90

Explanation

In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.

Which of the following can NOT be the angles of a triangle?

45, 45, 90

1, 2, 177

30.5, 40.1, 109.4

45, 90, 100

30, 60, 90

Explanation

In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.

Find the height of a triangle if the area of the triangle = 18 and the base = 4.

Explanation

The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.

Find the height of a triangle if the area of the triangle = 18 and the base = 4.

Explanation

The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.

$\text{Triangle A}$ and $\text{Triangle B}$ are similar triangles. The perimeter of Triangle A is 45” and the length of two of its sides are 15” and 10”. If the perimeter of Triangle B is 135” and what are lengths of two of its sides?

${30}''\textup{ and }{45}''$

${13}''\textup{ and }{19}''$

${20}''\textup{ and }{30}''$

${4}''\textup{ and }{6}''$

Explanation

The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.

Perimeter A = 45” and perimeter B = 135”

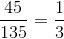
The proportion of Perimeter A to Perimeter B is $\frac{45}{135}=\frac{1}{3}$ .

This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.

15” x 3 = 45”

10” x 3 = 30“

Screen shot 2016 02 16 at 10.45.30 am

${30}''\textup{ and }{45}''$

${13}''\textup{ and }{19}''$

${20}''\textup{ and }{30}''$

${4}''\textup{ and }{6}''$

Explanation

The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.

Perimeter A = 45” and perimeter B = 135”

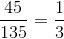
The proportion of Perimeter A to Perimeter B is $\frac{45}{135}=\frac{1}{3}$ .

This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.

15” x 3 = 45”

10” x 3 = 30“

Screen shot 2016 02 16 at 10.45.30 am

Equilateral

Figure is not drawn to scale.

Refer to the provided figure. Evaluate $m \angle CAD$ .

$18^{\circ }$

$8^{\circ }$

$13^{\circ}$

$23^{\circ }$

$28^{\circ }$

Explanation

$\bigtriangleup ABC$ is an equilateral, so all of its angles - in particular, $\angle ACB$ - measure $60^{\circ }$ . This angle is an exterior angle to $\bigtriangleup DAC$ , and its measure is equal to the sum of those of its two remote interior angles, $\angle DAC$ and $\angle D$ , so

$m\angle DAC + m\angle D = m \angle ACB$

Setting $m \angle ACB =60^{ \circ}$ and $m \angle D = 42^{\circ }$ , solve for $m\angle DAC$ :

$m\angle DAC + 42^{\circ }= 60^{\circ }$

$m\angle DAC = 60^{\circ } - 42^{\circ }= 18^{\circ }$

Equilateral

Figure is not drawn to scale.

Refer to the provided figure. Evaluate $m \angle CAD$ .

$18^{\circ }$

$8^{\circ }$

$13^{\circ}$

$23^{\circ }$

$28^{\circ }$

Explanation

$m\angle DAC + m\angle D = m \angle ACB$

Setting $m \angle ACB =60^{ \circ}$ and $m \angle D = 42^{\circ }$ , solve for $m\angle DAC$ :

$m\angle DAC + 42^{\circ }= 60^{\circ }$

$m\angle DAC = 60^{\circ } - 42^{\circ }= 18^{\circ }$

Triangle 2

Refer to the above figure. Evaluate $m \angle CDE$ .

$150 ^{\circ }$

$135^{\circ }$

$120^{\circ}$

$162 ^{\circ }$

$144^{\circ }$

Explanation

$\bigtriangleup ABC$ is marked with three congruent sides, making it an equilateral triangle, so $m \angle ABC = 60 ^{\circ }$ . This is an exterior angle of $\bigtriangleup BCD$ , making its measure the sum of those of its remote interior angles; that is,

$m \angle BCD + m \angle BDC = m \angle ABC$

$\bigtriangleup BCD$ has congruent sides $\overline{BC}$ and $\overline{CD}$ , so, by the Isosceles Triangle Theorem, $m \angle BCD = m \angle BDC$ . Substituting $m \angle BDC$ for $m \angle BCD$ and $60 ^{\circ }$ for $m \angle ABC$ :

$m \angle BDC + m \angle BDC = 60 ^{\circ }$

$2 \cdot m \angle BDC = 60 ^{\circ }$

$m \angle BDC = 30 ^{\circ }$

$\angle BDC$ and $\angle CDE$ form a linear pair and are therefore supplementary - that is, their degree measures total $180 ^{\circ }$ . Setting up the equation

$m \angle BDC + m\angle CDE= 180 ^{\circ }$

and substituting:

$30 ^{\circ } + m\angle CDE= 180 ^{\circ }$

$m\angle CDE= 150 ^{\circ }$

Triangle 2

Refer to the above figure. Evaluate $m \angle CDE$ .

$150 ^{\circ }$

$135^{\circ }$

$120^{\circ}$

$162 ^{\circ }$

$144^{\circ }$

Explanation

$m \angle BCD + m \angle BDC = m \angle ABC$

$m \angle BDC + m \angle BDC = 60 ^{\circ }$

$2 \cdot m \angle BDC = 60 ^{\circ }$

$m \angle BDC = 30 ^{\circ }$

$\angle BDC$ and $\angle CDE$ form a linear pair and are therefore supplementary - that is, their degree measures total $180 ^{\circ }$ . Setting up the equation

$m \angle BDC + m\angle CDE= 180 ^{\circ }$

and substituting:

$30 ^{\circ } + m\angle CDE= 180 ^{\circ }$

$m\angle CDE= 150 ^{\circ }$

Page 1 of 6

Return to subject