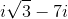Complex Numbers
Help Questions
SAT Math › Complex Numbers


The correct answer is not listed.
Explanation
This gives us roots of
The product of 
The sum of these 4 is:
What we notice is that each of the roots has a negative. It thus makes sense that they will all cancel out. Rather than going through all the multiplication, we can instead look at the very beginning setup, which we can simplify using the distributive property:
Simplify:
Explanation
Use FOIL:
Combine like terms:
But since 
Find the product of (3 + 4i)(4 - 3i) given that i is the square root of negative one.
7 + i
0
12 - 12i
24
24 + 7i
Explanation
Distribute (3 + 4i)(4 - 3i)
3(4) + 3(-3i) + 4i(4) + 4i(-3i)
12 - 9i + 16i -12i2
12 + 7i - 12(-1)
12 + 7i + 12
24 + 7i
Simplify:
Explanation
Rewrite 


The correct answer is not listed.
Explanation
This gives us roots of
The product of 
The sum of these 4 is:
What we notice is that each of the roots has a negative. It thus makes sense that they will all cancel out. Rather than going through all the multiplication, we can instead look at the very beginning setup, which we can simplify using the distributive property:
Simplify:
Explanation
Rewrite 
Find the product of (3 + 4i)(4 - 3i) given that i is the square root of negative one.
7 + i
0
12 - 12i
24
24 + 7i
Explanation
Distribute (3 + 4i)(4 - 3i)
3(4) + 3(-3i) + 4i(4) + 4i(-3i)
12 - 9i + 16i -12i2
12 + 7i - 12(-1)
12 + 7i + 12
24 + 7i
Define an operation 

If 

Explanation



Rationalize the denominator by multiplying both numerator and denominator by the complex conjugate of the latter, which is 
Define an operation 

If 

Explanation



Rationalize the denominator by multiplying both numerator and denominator by the complex conjugate of the latter, which is 
Simplify:
Explanation
Use FOIL:
Combine like terms:
But since 










![[(-2+5i) + (2-5i)] + [(5+2i) + (-5-2i)] =](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26403/gif.latex)
![=[(-2)+2 +5i - 5i] + [5-5 + 2i - 2i] = [0] + [0] = 0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26404/gif.latex)
![1(5+2i) + (-1)\cdot(5+2i)+ i(5+2i)+(-i) \cdot(5+2i) = (5+2i)\cdot[1+(-1)+i+(-i)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26405/gif.latex)
![= (5+2i)\cdot[0] = 0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26406/gif.latex)