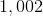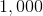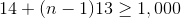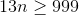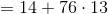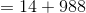Arithmetic Sequences
Help Questions
SAT Math › Arithmetic Sequences
An arithmetic sequence begins as follows: 14, 27, 40...
What is the first four-digit integer in the sequence?
Explanation
Given the first two terms 


Setting 

The 
Since we are looking for the first four-digit whole number - equivalently, the first number greater than or equal to 1,000:
Setting 


Therefore, the 77th term, or 




the correct choice.
An arithmetic sequence begins as follows:
Give the first integer in the sequence.
The sequence has no integers.
Explanation
Rewrite all three fractions in terms of their least common denominator, which is 


The sequence begins
Subtract the first term 


Setting 

If this common difference is added a few more times, a pattern emerges:

All of the denominators end in 4 or 9, so none of them can be divisible by 20. Therefore, none of the terms will be integers.
An arithmetic sequence begins as follows: 14, 27, 40...
What is the first four-digit integer in the sequence?
Explanation
Given the first two terms 


Setting 

The 
Since we are looking for the first four-digit whole number - equivalently, the first number greater than or equal to 1,000:
Setting 


Therefore, the 77th term, or 




the correct choice.
An arithmetic sequence begins as follows:
What is the first positive number in the sequence?
The twentieth term
The twenty-first term
The twenty-second term
The twenty-third term
The nineteenth term
Explanation
Given the first two terms 


Setting 

The 
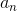
Since we are looking for the first positive number - equivalently, the first number greater than 0:


Setting 


Since 



An arithmetic sequence begins as follows: 14, 27, 40...
What is the first four-digit integer in the sequence?
Explanation
Given the first two terms 


Setting 

The 
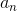
Since we are looking for the first four-digit whole number - equivalently, the first number greater than or equal to 1,000:
Setting 


Therefore, the 77th term, or 




the correct choice.
An arithmetic sequence begins as follows:
Give the sixteenth term of this sequence.
None of the other responses give the correct answer.
Explanation
Subtract the first term 


Setting 
The 
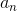
Setting 


An arithmetic sequence begins as follows:
What is the first positive number in the sequence?
The twentieth term
The twenty-first term
The twenty-second term
The twenty-third term
The nineteenth term
Explanation
Given the first two terms 


Setting 

The 
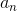
Since we are looking for the first positive number - equivalently, the first number greater than 0:


Setting 


Since 



An arithmetic sequence begins as follows:
What is the first positive number in the sequence?
The twentieth term
The twenty-first term
The twenty-second term
The twenty-third term
The nineteenth term
Explanation
Given the first two terms 


Setting 

The 
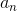
Since we are looking for the first positive number - equivalently, the first number greater than 0:


Setting 


Since 



An arithmetic sequence begins as follows:
Give the first integer in the sequence.
The sequence has no integers.
Explanation
Rewrite all three fractions in terms of their least common denominator, which is 


The sequence begins
Subtract the first term 


Setting 

If this common difference is added a few more times, a pattern emerges:

All of the denominators end in 4 or 9, so none of them can be divisible by 20. Therefore, none of the terms will be integers.
An arithmetic sequence begins as follows:
Give the sixteenth term of this sequence.
None of the other responses give the correct answer.
Explanation
Subtract the first term 


Setting 
The 
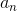
Setting