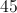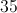Other Polygons
Help Questions
SAT Math › Other Polygons
A regular seven sided polygon has a side length of 14”. What is the measurement of one of the interior angles of the polygon?
128.57 degrees
257.14 degrees
180 degrees
154.28 degrees
252 degrees
Explanation
The formula for of interior angles based on a polygon with a number of side n is:
Each Interior Angle = (n-2)*180/n
= (7-2)*180/7 = 128.57 degrees
A regular seven sided polygon has a side length of 14”. What is the measurement of one of the interior angles of the polygon?
128.57 degrees
257.14 degrees
180 degrees
154.28 degrees
252 degrees
Explanation
The formula for of interior angles based on a polygon with a number of side n is:
Each Interior Angle = (n-2)*180/n
= (7-2)*180/7 = 128.57 degrees
What is the measure, in degrees, of each interior angle of a regular convex polygon that has twelve sides?
120
135
150
175
180
Explanation
The sum of the interior angles, in degrees, of a regular polygon is given by the formula 180(n – 2), where n is the number of sides. The problem concerns a polygon with twelve sides, so we will let n = 12. The sum of the interior angles in this polygon would be 180(12 – 2) = 180(10) = 1800.
Because the polygon is regular (meaning its sides are all congruent), all of the angles have the same measure. Thus, if we divide the sum of the measures of the angles by the number of sides, we will have the measure of each interior angle. In short, we need to divide 1800 by 12, which gives us 150.
The answer is 150.
What is the measure, in degrees, of each interior angle of a regular convex polygon that has twelve sides?
120
135
150
175
180
Explanation
The sum of the interior angles, in degrees, of a regular polygon is given by the formula 180(n – 2), where n is the number of sides. The problem concerns a polygon with twelve sides, so we will let n = 12. The sum of the interior angles in this polygon would be 180(12 – 2) = 180(10) = 1800.
Because the polygon is regular (meaning its sides are all congruent), all of the angles have the same measure. Thus, if we divide the sum of the measures of the angles by the number of sides, we will have the measure of each interior angle. In short, we need to divide 1800 by 12, which gives us 150.
The answer is 150.
What is the average (arithmetic mean) of all 15 interior angles of a quadrilateral, pentagon, and hexagon?
Explanation
The 4 angles of a quadrilateral add to 360
The 5 angles of a pentagon add to 540
The 6 angles of a hexagon add to 720
Find the sum of the interior angles in a nonagon.
Explanation
To solve, simply use the formula for the total degrees in a polygon, where n is the number of vertices.
In this particular case, a nonagon is a shape with nine sides and thus nine vertices.
Thus,
What is the measure of each central angle of an octagon?
Explanation
There are 360 degrees and 8 angles, so dividing leaves 45 degrees per angle.
What is the measure of each central angle of an octagon?
Explanation
There are 360 degrees and 8 angles, so dividing leaves 45 degrees per angle.
Find the sum of the interior angles in a nonagon.
Explanation
To solve, simply use the formula for the total degrees in a polygon, where n is the number of vertices.
In this particular case, a nonagon is a shape with nine sides and thus nine vertices.
Thus,
What is the average (arithmetic mean) of all 15 interior angles of a quadrilateral, pentagon, and hexagon?
Explanation
The 4 angles of a quadrilateral add to 360
The 5 angles of a pentagon add to 540
The 6 angles of a hexagon add to 720