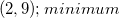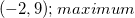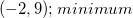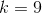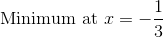Maximum and Minimum

Help Questions

SAT Math › Maximum and Minimum

Questions 1 - 4

1

What is the vertex of ? Is it a max or min?

$-\frac{5}{6}, \textup{Max}$

$-\frac{5}{6}, \textup{Min}$

$-\frac{5}{3}, \textup{Max}$

$-\frac{5}{3}, \textup{Min}$

$\frac{5}{6}, \textup{Min}$

Explanation

The polynomial is in standard form of a parabola.

To determine the vertex, first write the formula.

$x=-\frac{b}{2a}$

Substitute the coefficients.

$x=-\frac{-5}{2(-3)} = -\frac{5}{6}$

Since the is negative is negative, the parabola opens down, and we will have a maximum.

The answer is: $-\frac{5}{6}, \textup{Max}$

2

Given the parabola equation , what is the max or minimum, and where?

$\textup{Max}, (\frac{2}{3}, \frac{4}{3})$

$\textup{Min}, (\frac{2}{3}, \frac{4}{3})$

$\textup{Max}, (\frac{2}{3},4)$

$\textup{Max}, (-\frac{2}{3},-4)$

$\textup{Min}, (-\frac{2}{3},-4)$

Explanation

The parabola is in the form:

The vertex formula will determine the x-value of the max or min. Since the value of is negative, the parabola will open downward, and there will be a maximum.

Write the vertex formula and substitute the correct coefficients.

$x=-\frac{b}{2a} = -\frac{4}{2(-3)} = \frac{2}{3}$

Substitute this value back in the parabolic equation to determine the y-value.

$y=-3( \frac{2}{3})^2+4( \frac{2}{3}) = \frac{4}{3}$

The answer is: $\textup{Max}, (\frac{2}{3}, \frac{4}{3})$

3

What is the vertex of the following function? Is it a maximum or a minimum?

$\small f(x) = -3(x-2)^2+9$

$\small \small (2,9); maximum$

$\small (2,9); minimum$

$\small (-2,9); maximum$

$\small (-2,9); minimum$

$\small (2,-9); maximum$

Explanation

The equation of a parabola can be written in vertex form

$\small f(x) = a(x-h)^2+k$

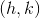
where $\small \tiny (h,k)$ is the vertex and $\tiny a$ determines if it is a minimum or maximum. If $\tiny a$ is positive, then it is a minimum; if $\tiny a$ is negative, then it is a maximum.

$\small \small f(x)=-3(x-2)^2+9$

In this example, $\small \small a$ is negative, so the vertex is a maximum.

$\small h = 2$ and $\small k=9$

$\small (h,k)=(2,9)$

4

Determine the maximum or minimum of .

$\textup{Maximum at }x=\frac{1}{3}$

$\textup{Minimum at }x=\frac{2}{3}$

$\textup{Minimum at }x=-\frac{1}{3}$

$\textup{Maximum at }x=-\frac{1}{3}$

$\textup{Maximum at }x=-3$

Explanation

Rewrite the equation by the order of powers.

This is a parabola in standard form:

Determine the values of 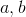to the vertex formula.

$x=-\frac{b}{2a}=-\frac{6}{2(-9)}= \frac{6}{18}=\frac{1}{3}$

Since the leading coefficient of the parabola is negative, the parabola will curve downward and will have a maximum point.

Therefore there is a maximum at,

$x=\frac{1}{3}$ .

Return to subject