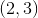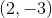Midpoint Formula
Help Questions
SAT Math › Midpoint Formula
Find the midpoint of the line that passes through the points 

Explanation
Recall the midpoint formula as 
Thus,
Find the midpoint of the line segment with endpoints 

Explanation
Use the midpoint formula:
Substitute:
The midpoint is
What is the midpoint of a line that connects the points 

Explanation
The midpoint formula is 
Therefore, all we need to do is plug in the points given to us to find the midpoint.
In this case, 
To find the 



To find the 



So our solution is 
What is the coordinates of the point exactly half way between (-2, -3) and (5, 7)?
Explanation
We need to use the midpoint formula to solve this question.
In our case
and
Therefore, substituting these values in we get the following:
Find the midpoint of the line that passes through the points 

Explanation
Recall the midpoint formula as 
Thus,
Find the midpoint of a line with the endpoings (3, 4) and (-1, -1).
Explanation
When finding the midpoint between two points, we use the midpoint formula
where 

Knowing this, we can substitute the values into the formula. We get
Therefore, 
Find the point halfway between points A and B.
Explanation
Find the point halfway between points A and B.
We are going to need to use midpoint formula. If you ever have difficulty recalling midpoint formula, try to recall that it is basically taking two averages. One average is the average of your x values, the other average is the average of your y values.
Now we plug and chug!
So our answer is (43,44)
What is the midpoint between 

Explanation
The formula to find the midpoint is as follows:
In our case our
our
substituting in these values we get
midpoint =
Find the midpoint between 

Explanation
Write the midpoint formula.
Substitute the points.
The answer is:
Find the midpoint between 

Explanation
Write the formula for the midpoint.
Substitute the point into the formula.
The answer is: