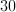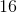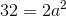Isosceles Triangles
Help Questions
SAT Math › Isosceles Triangles
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
100
100√2
50√2
50
200√2
Explanation
The length of the diagonal of a given square is 
Explanation
If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse.
We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles.
Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say:
Now, solve for the unknown:

This means that the length of the sides of our triangle, as well as the sides of our square, is 
To find the area of the square, do the following:

The length of the diagonal of a given square is 
Explanation
If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse.
We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles.
Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say:
Now, solve for the unknown:

This means that the length of the sides of our triangle, as well as the sides of our square, is 
To find the area of the square, do the following:

What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
100
100√2
50√2
50
200√2
Explanation
A triangle has the following side lengths:
Which of the following correctly describes the triangle?
Acute and isosceles
Obtuse and isosceles
Acute and scalene
Obtuse and scalene
None of these
Explanation
The triangle has two sides of equal length, 13, so it is by definition isosceles.
To determine whether the triangle is acute, right, or obtuse, compare the sum of the squares of the lengths of the two shortest sides to the square of the length of the longest side. The former quantity is equal to
The latter quantity is equal to
The former is greater than the latter; consequently, the triangle is acute. The correct response is that the triangle is acute and isosceles.
The length of the diagonal of a given square is 
Explanation
If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse.
We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles.
Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say:
Now, solve for the unknown:

This means that the length of the sides of our triangle, as well as the sides of our square, is 
To find the area of the square, do the following:

What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
100
100√2
50√2
50
200√2
Explanation
A triangle has the following side lengths:
Which of the following correctly describes the triangle?
Acute and isosceles
Obtuse and isosceles
Acute and scalene
Obtuse and scalene
None of these
Explanation
The triangle has two sides of equal length, 13, so it is by definition isosceles.
To determine whether the triangle is acute, right, or obtuse, compare the sum of the squares of the lengths of the two shortest sides to the square of the length of the longest side. The former quantity is equal to
The latter quantity is equal to
The former is greater than the latter; consequently, the triangle is acute. The correct response is that the triangle is acute and isosceles.