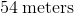SAT Math - How to find the perimeter of a rectangle

Find the perimeter of a rectangle with width 6 and length 9.

Explanation

To solve, simply use the formula for the perimeter.

Another way to solve this problem is to add up all of the sides. Remember that even though only two values are given, a rectangle has 4 sides. Thus,

A rectangular garden has an area of $80: \mbox{m^2}$ . Its length is meters longer than its width. How much fencing is needed to enclose the garden?

$40: \mbox{meters}$

$18: \mbox{meters}$

$24: \mbox{meters}$

$36: \mbox{meters}$

$54: \mbox{meters}$

Explanation

We define the variables as $w = \mbox{width}$ and $l = \mbox{length} = w + 2$ .

We substitute these values into the equation for the area of a rectangle and get $A_{\mbox{rectangle} }= wl = w(w + 2) = 80$ .

Lengths cannot be negative, so the only correct answer is . If , then .

Therefore, $\mbox{perimeter }= 2w + 2l = 16 + 20 = 36:\mbox{m}$ .

Three of the vertices of a rectangle on the coordinate plane are located at the origin, , and . Give the perimeter of the rectangle.

Explanation

The rectangle in question is below:

Rectangle 3

The lengths of the rectangle is 10, the distance from the origin to ; its width is 7, the distance from the origin to . The perimeter of a rectangle is equal to twice the sum of its length and width, so calculate:

$P= 2 (10+ 7 ) = 2 \times 17 = 34$ .

You have a poster of one of your favorite bands that you are planning on putting up in your dorm room. If the poster is 3 feet tall by 1.5 feet wide, what is the perimeter of the poster?

Explanation

You have a poster of one of your favorite bands that you are planning on putting up in your dorm room. If the poster is 3 feet tall by 1.5 feet wide, what is the perimeter of the poster?

Perimeter of a rectangle is found via: