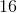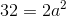If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse.

We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles.

Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say:

Now, solve for the unknown:

.

This means that the length of the sides of our triangle, as well as the sides of our square, is .

To find the area of the square, do the following:

.