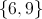SAT Math - How to find the intersection of a Venn Diagram

Venn 1

In the above Venn diagram, let the universal set be

$U =\left { 1, 2, 3, ...40 \right }$

$A = \left { x | x$ yields a remainder of 1 when divided by 4 $\left \right }$

$B = \left { x | x$ yields a remainder of 1 when divided by 3 $\left \right }$

How many elements of would be placed in the shaded portion of the above diagram?

Six

Seven

Eight

Nine

Five

Explanation

The shaded portion of the Venn diagram is $A \cap B'$ - the set of all elements in but not .

The following elements of yield a remainder of 1 when divided by 4, and therefore comprise set :

$A = \left { 1, 5, 9, 13, 17, 21, 25, 29, 33, 37 \right }$

If 3 is subtracted from each, what results are the elements whose division by 4 yields a remainder of 1, and thus, elements of .

The following elements of yield a remainder of 1 when divided by 4, and therefore comprise set :

$B = \left { 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40 \right }$

The elements in that are also elements in are 1, 13, 25, and 37 - four elements out of ten. Therefore, the set $A \cap B'$ comprises six elements.

$Set\ A=\left { 2,4,6,8,10,12 \right }$ and $Set\ B=\left { 5,6,7,8,9 \right }$ .

Find $A\bigcap B$ .

$\left { 6,8 \right }$

$\left { 6,9 \right }$

$\left { \ \right }$

$\left {5,7,9 \right }$

$\left {6,7,8 \right }$

Explanation

The intersection of two sets contains every element that is present in both sets, so $\left { 6,8 \right }$ is the correct answer.

What is the intersection of the Venn Diagram shown below?

Screen shot 2015 10 27 at 3.45.31 pm

Explanation

The intersection of the Venn Diagram is only the numbers in both circles.

The section in the middle contains the answer set.

Thus the intersection is, .

Set A contains the positive even integers less than 14. Set B contains the positive multiples of three less than 20. What is the intersection of the two sets?

A∩B = { }

A∩B = {6, 12}

A∩B = {4, 6, 8}

A∩B = {6}

A∩B = {6, 12, 18}

Explanation

A = {2, 4, 6, 8, 10, 12}

B = {3, 6, 9, 12, 15, 18}

The intersection of a set means that the elements are in both sets: A∩B = {6, 12}

We have two sports clubs offered to a class of 100 students. 70 students joined the basketball club, 40 students joined the swimming club, and 10 students joined neither. How many students joined both the swimming club and the basketball club?

Explanation

The idea is to draw a Venn Diagram and find the intersection. We have one circle of 70 and another with 40. When we add the two circles plus the 10 students who joined neither, we should get 100 students. However, when adding the two circles, we are adding the intersections twice, therefore we need to subtract the intersection once.

We get , which means the intersection is 20.

There are 75 juniors at a high school. 15 of the students are enrolled in Physics and 40 students are enrolled in Chemistry. 30 students are not enrolled in either Physics or Chemistry. How many students are enrolled in both Physics and Chemistry?

Explanation

First, subtract the students that are in neither class; 75 – 30 = 45 students.

Thus, 45 students are enrolled in Chemistry, Physics, or both. Of these 45 students, we know 40 are in Chemistry, so that leaves 5 students who are enrolled in Physics only; with 15 total students in Physics, that means 10 must be in Chemistry as well. So 10 students are in both Physics and Chemistry.

Students at a local high school are given the option to take one gym class, one music class or one of each. Out of 100 students, 60 say that they are currently taking a gym class and 70 say that they are taking a music class. How many students are taking both?

Explanation

This problem can be solved two ways, with a formula or with reason.

Using the formula, the intersection of the Venn diagram for which classes students take is:

By using reason, it is clear that 60 + 70 is greater than 100 by 30. It is assumed that this extra 30 students come from students who were counted twice because they took both classes.

Let Set A = $\left { 1, 2, 4, 6, 7, 10\right }$ and Set B = $\left {2, 4, 5, 6, 8, 9, 10 \right }$ .

Find $A\bigcap B$ .

$\left { 2, 4, 6, 10\right }$

$\left { 2, 4, 5, 6, 7, 10\right }$

$\left {4, 6, 10\right }$

$\left { 2, 4, 5, 7, 10\right }$

$\left { 2\right }$

Explanation

$A\bigcap B$ represents the intersection of the two sets. In other words, we want all the elements that appear in both sets. The elements that appear in both sets are 2, 4, 6, and 10.

Therefore, $A\bigcap B=\left { 2, 4, 6, 10\right }$

Fifty 6th graders were asked what their favorite school subjects were. Three students like math, science and English. Five students liked math and science. Seven students liked math and English. Eight people liked science and English. Twenty students liked science. Twenty-eight students liked English. Fourteen students liked math. How many students didn’t like any of these classes?

None of the answers are correct

Explanation

Draw a Venn diagram with three subsets: Math, Science, and English. Start in the center with students that like all three subjects. Next, look at students that liked two subjects. Be sure to subtract out the ones already counted in the middle. Then, look at the students that only like one subject. Be sure to subtract out the students already accounted for. Once all of the subsets are filled, look at those students who don’t like any of these subjects. To find the students who don’t like any of these subjects add all of the students who like at least one subject from the total number of students surveyed, which is 50.

M = math

S = science

E = English

M∩S∩E = 3

M∩S = 5 (but 3 are already accounted for) so 2 for M and S ONLY

M∩E = 7 (but 3 are already accounted for) so 4 for M and E ONLY

S∩E = 8 (but 3 are already accounted for) so 5 for S and E ONLY

M = 14 (but 3 + 2 + 4 are already accounted for) so 5 for M ONLY

S = 20 (but 3 + 2 + 5 are already accounted for) so 10 for S ONLY

E = 28 (but 3 + 4 + 5 are already accounted for) so 16 for E ONLY

Therefore, the students already accounted for is 3 + 2 +4 + 5 + 5 + 10 + 16 = 45 students

So, those students who don’t like any of these subjects are 50 – 45 = 5 students

Farmer John has one hundred plots of land. Sixty plots grow corn. Forty plots grow carrots. These numbers take into account that some of the plots grow both corn and carrots.

How many plots grow both corn and carrots?