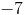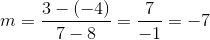SAT Math - How to find slope of a line

What is the slope of a line which passes through coordinates $\dpi{100} \small (3,7)$ and $\dpi{100} \small (4,12)$ ?

$\dpi{100} \small 5$

$\dpi{100} \small \frac{1}{5}$

$\dpi{100} \small \frac{1}{2}$

$\dpi{100} \small 2$

$\dpi{100} \small 3$

Explanation

Slope is found by dividing the difference in the $\dpi{100} \small y$ -coordinates by the difference in the $\dpi{100} \small x$ -coordinates.

$\dpi{100} \small \frac{(12-7)}{(4-3)}=\frac{5}{1}=5$

What is the slope of a line that runs through points: (-2, 5) and (1, 7)?

2/3

5/7

3/2

Explanation

The slope of a line is defined as a change in the y coordinates over a change in the x coordinates (rise over run).

To calculate the slope of a line, use the following formula: Actmath_7_113_q7

What is the slope of a line that passes though the coordinates $(5,2)$ and $(3,1)$ ?

$\frac{1}{2}$

$-\frac{1}{2}$

$-\frac{2}{3}$

$\frac{2}{3}$

$4$

Explanation

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{1-2}{3-5}=\frac{-1}{-2}=\frac{1}{2}$

What is the slope of a line running through points and ?

$-\frac{1}{7}$

$\frac{7}{3}$

Explanation

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{3-(-4)}{7-8}=\frac{7}{-1}=-7$

A line passes through the points (–3, 5) and (2, 3). What is the slope of this line?

–2/3

–2/5

2/5

2/3

-3/5

Explanation

The slope of the line that passes these two points are simply ∆y/∆x = (3-5)/(2+3) = -2/5

Which of the following lines intersects the y-axis at a thirty degree angle?

y = x

y = x - √2

y = x√2 - 2

y = x√3 + 2

y = x((√3)/3) + 1

Explanation

Line_intersect1

Line_intersect2

What is a possible slope of line y?

–2

$\dpi{100} \small \frac{1}{2}$

$\dpi{100} \small -\frac{1}{2}$

Explanation

The slope is negative as it starts in quadrant 2 and ends in quadrant 4. Slope is equivlent to the change in y divided by the change in x. The change in y is greater than the change in x, which implies that the slope must be less than –1, leaving –2 as the only possible solution.

What is the slope between and ?