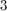SAT Math - How to factor a number

What is the product of the distinct prime factors of 24?

$\dpi{100} \small 6$

$\dpi{100} \small 8$

$\dpi{100} \small 9$

$\dpi{100} \small 24$

$\dpi{100} \small 5$

Explanation

The prime factorization of 24 is (2)(2)(2)(3). The distinct primes are 2 and 3, the product of which is 6.

If the variable x is an integer divisible by the numbers 2 and 3, which of the following is necessarily divisible by 2, 3 and 5?

5x + 2

x + 30

2x + 30

6x + 30

5x + 30

Explanation

For this question, use the fact that a sum of two multiples is a multiple. In other words:

if x is a multiple of 3 and y is a multiple of 3: (x + y) is a multiple of 3.

Thus in this question, x is a multiple of 2 and 3. We need to find a number that is a multiple of 2, 3, and 5.

Take 5x + 30:

\[x is divisible by 2. 5 times x is still divisble by 3. 30 is divisible by 2.\] -> divisible by 2.

\[x is divisible by 3. 5 times x is still divisble by 3. 30 is divisible by 3.\] -> divisible by 3.

\[5x is divisible by 5. 30 is divisible by 5.\] -> divisible by 5.

Thus 5x + 30 is divisible by 2, 3 and 5.

What is the sum of all prime factors of 152?

Explanation

Since 152 is divisible by 2, start by dividing 152 by 2 which gives you factors of 2 and 76. 2 is a prime factor (cannot be divisible by anything other than itself and 1) but 76 can still be divided by 2. Continue dividing until there are only prime factors. You should get prime factors of 2, 2, 2, and 19. 2+2+2+19 = 25.

If p is an integer, then which of the following could be equal to (6 + 2p)(3)

Explanation

Let n represent all of the numbers that are equal to (6 + 2p)(3). Then, let's solve for p in terms of n.

(6 + 2p)(3) = n

Divide both sides by 3.

(6 + 2p) = n/3

Subtract six from both sides.

2p = –6 + n/3

Divide both sides by 2.

p = –3 + n/6

Since we are told that p is an integer, the only way that p can be an integer is if n is a multiple of 6. Only a multiple of six, when divided by six, will yield an integer number. Any integer plus –3 will also be an integer, since the sum of two integers is always an integer.

In short, we must look for the answer choice that is a multiple of 6. Of the choices, only 84 is a multiple of 6.

The answer is 84.

If $180 = 2^{a}3^{b}5^{c}7^{d}$ , where $a,b,c,d$ are all positive integers, what is $a+b+c+d$ ?

Explanation

We will essentially have to represent 180 as a product of prime factors, because 2, 3, 5, and 7 are all prime numbers. The easiest way to do this will be to find the prime factorization of 180.

180 = 18(10)= (9)(2)(10) = (3)(3)(2)(10)=(3)(3)(2)(2)(5) = $2^{2}3^{2}5^{1}$ . Because 7 is not a factor of 180, we can mutiply the prime factorization of 180 by $7^{0}$ (which equals 1) in order to get 7 into our prime factorization.

$180=$ $2^23^25^17^0$ = $2^a3^b5^c7^d$

In order for $2^23^25^17^0$ to equal $2^a3^b5^c7^d$ , the exponents of each base must match. This means that a = 2, b = 2, c = 1, and d = 0. The sum of a, b, c, and d is 5.

The answer is 5.

If p is a prime number greater than 1, how many positive factors does p4 have?

Two

Three

Four

Five

Six

Explanation

3 is a prime number that is easy to work with, so we can plug that in for p. p4 = 81. The positive factors of 81 are 1, 3, 9, 27, and 81. Thus, the answer is five factors.

Let's look at another prime number to plug in for p. If we plug in 2, another easy prime number to work woth, we get p4 = 16. The positive factors of 16 are 1, 2, 4, 8 and 16.

Notice that when p = prime number greater than 1, the positive factors for p4 are 1, p, p2, p3 and p4. Multiplying pn by p only adds pn as a factor when p is prime, so you will have n factors plus 1 which is a factor, so p4 has 5 factors.

If there are to be parking spaces at least 6 feet wide along a wall 46 feet long, how many parking space can be drawn in?