How to evaluate a fraction
Help Questions
SAT Math › How to evaluate a fraction
Solve the following:
Explanation
In order to subtract the fractions, the denominator must be the same. The common denominator is 9. Rewrite the fractions.
Evaluate the following equation when 
Explanation
1. Plug in 

2. Perform the above operations.
Evaluate:
Explanation
Find the least common denominator, or LCD of 
Rewrite the equation with the correct denominator.
Multiply by six on both sides of the equation and solve for 
Solve:
Explanation
In order to solve 
Rewrite the equation.
Multiply by six on both sides of the equation to cancel the denominators.
Solve 
0
–1
no solution
infinitely many solutions
Explanation
The common denominator of the left side is x(x–1). Multiplying the top and bottom of 1/x by (x–1) yields




Since this statement is true, there are infinitely many solutions.
If 



Explanation
In order to solve 




Then:
Finally:
With the values of 


Simplify:
Explanation
Begin by simplifying the numerator and the denominator.
Numerator


Denominator


Now, reconstructing our fraction, we have:
To make this division work, you multiply the numerator by the reciprocal of the denominator:
For this question, the following trigonometric identities apply:

Simplify:
Explanation
To begin a problem like this, you must first convert everything to 

Since 

From here we combine the numerator and denominators of each fraction together to easily see what we can combine and cancel.
Since there is a 

If 3x = 12, y/4 = 10, and 4z = 9, what is the value of (10xyz)/xy?
10
4 1/2
360
160
22 1/2
Explanation
Solve for the variables, the plug into formula.
x = 12/3 = 4
y = 10 * 4 = 40
z= 9/4 = 2 1/4
10xyz = 3600
Xy = 160
3600/160 = 22 1/2
If 

Explanation
To raise 






























































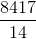


















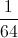
![w^\frac{2}{3}=\sqrt[3]{w^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177545/gif.latex)
![(\frac{1}{8})^\frac{2}{3}=\sqrt[3]{(\frac{1}{8})^2}=\sqrt[3]{\frac{1}{64}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177546/gif.latex)
![\sqrt[3]{\frac{1}{64}}=\frac{1}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177547/gif.latex)
