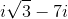SAT Math - How to add complex numbers

Simplify: $\sqrt{-3}+\sqrt{-9}+\sqrt{-16}$

$i\sqrt3 +7i$

$i\sqrt3 -7i$

$i\sqrt3-i$

$i\sqrt3 +i$

$2i\sqrt7$

Explanation

Rewrite $\sqrt{-3}+\sqrt{-9}+\sqrt{-16}$ in their imaginary terms.

$i=\sqrt{-1}$

$\sqrt{-3}+\sqrt{-9}+\sqrt{-16}=i\sqrt3+3i+4i = i\sqrt3 +7i$

Evaluate:

$i^{6} + i^{7}+ i^{8}+ i^{9}$

Explanation

A power of can be evaluated by dividing the exponent by 4 and noting the remainder. The power is determined according to the following table:

$\begin{matrix} \textrm{\underline{Rem}}& \textrm{\underline{Power}} \ 0& 1\ 1& i\ 2& -1\ 3& -i \end{matrix}$

$6 \div 4 = 1 \textrm{ R }2$ , so $i^{6} = -1$

$7 \div 4 = 1 \textrm{ R }3$ , so $i^{7} = -i$

$8 \div 4 = 2 \textrm{ R }0$ , so $i^{8} = 1$

$9 \div 4 = 2 \textrm{ R }1$ , so $i^{9} = i$

Substituting:

$i^{6} + i^{7}+ i^{8}+ i^{9}$

Add $5 + i \sqrt {5 }$ and its complex conjugate.

$2 i \sqrt{5}$

$-2 i \sqrt{5}$

Explanation

The complex conjugate of a complex number is . Therefore, the complex conjugate of $5 + i \sqrt {5 }$ is $5 - i \sqrt {5 }$ ; add them by adding real parts and adding imaginary parts, as follows:

$(5 + i \sqrt {5 } )+( 5 - i \sqrt {5 })$

$= 5 + 5 + i \sqrt {5 } - i \sqrt {5 }$

the correct response.

Add $13 - i \sqrt{13}$ to its complex conjugate.

$2i \sqrt{13}$

$-2i \sqrt{13}$

Explanation

The complex conjugate of a complex number is . Therefore, the complex conjugate of $13 - i \sqrt{13}$ is $13 + i \sqrt{13}$ ; add them by adding real parts and adding imaginary parts, as follows:

$(13 - i \sqrt{13} )+( 13 + i \sqrt{13})$

$= 13+13 - i \sqrt {13 }+ i \sqrt {13}$

Simplify:

Explanation

It can be easier to line real and imaginary parts vertically to keep things organized, but in essence, combine like terms (where 'like' here means real or imaginary):

Evaluate:

$9i^{9}+ 10 i^{10}+ 11 i^{11}+ 12 i^{12}$

None of these

Explanation

A power of can be evaluated by dividing the exponent by 4 and noting the remainder. The power is determined according to the following table:

$\begin{matrix} \textrm{\underline{Rem}}& \textrm{\underline{Power}} \ 0& 1\ 1& i\ 2& -1\ 3& -i \end{matrix}$

$9 \div 4 = 2 \textrm{ R }1$ , so $i^{9} = i$

$10 \div 4 = 2 \textrm{ R }2$ , so $i^{10} = -1$

$11 \div 4 = 2 \textrm{ R }3$ , so $i^{11} = - i$

$12 \div 4 = 3 \textrm{ R }0$ , so $i^{12} = 1$

Substituting:

$9i^{9}+ 10 i^{10}+ 11 i^{11}+ 12 i^{12}$

Collect real and imaginary terms:

For $i=\sqrt{-1}$ , what is the sum of $\frac{3}{2} + \frac{1}{4} i$ and its complex conjugate?

$\frac{1}{2} i$

$-\frac{1}{2} i$

$\frac{7}{4} + \frac{7}{4} i$

Explanation

The complex conjugate of a complex number is , so $\frac{3}{2} + \frac{1}{4} i$ has $\frac{3}{2} - \frac{1}{4} i$ as its complex conjugate. The sum of the two numbers is