Exponents and Logarithms
Help Questions
SAT Math › Exponents and Logarithms
Simplify:
Explanation
When adding exponents, we don't add the exponents or multiply out the bases. Our goal is to see if we can factor anything. We do see three 

Give the set of real solutions to the equation
(round to the nearest hundredth, if applicable)
Explanation
Using the Product of Powers Rule, then the Power of a Power Rule, rewrite the first term:
Substitute 


which is quadratic in terms of 



Factoring by grouping:
By the Zero Product Rule, one of these two factors must be equal to 0.
If 

Substituting 


This is impossible, since any power of a positive number must be positive.
If 
Substituting 

Since 
it holds that 

Simplify:
Explanation
When dealing with subtraction in regards to logarithms, it's the same as dividing the numbers.
Explanation
By the Power of a Power and Product of Power Rules, we can rewrite this equation as
Substitute 


which can be written in standard form by subtracting 
The quadratic trinomial fits the perfect square trinomial pattern:
By the square root principle,
Substituting 

How many elements are in a set that has exactly 128 subsets?
None of the other responses is correct.
Explanation
A set with 

Solve:
Solve for 
No solution
Explanation

can be rewritten as:
By the Power of a Power rule:
It follows that
Solving for 
Simplify:
Explanation
When dealing with addition in regards to logarithms, it's the same as multiplying the numbers.
Simplify:
Explanation





Rewrite as a single logarithmic expression:
Explanation
Using the properties of logarithms


we simplify as follows:
Solve and simplify.
Explanation
![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/671898/gif.latex)



















































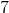
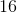












































![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/671897/gif.latex)



![5\sqrt[3]{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/671871/gif.latex)
