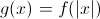Transformation
Help Questions
SAT Math › Transformation
Line m passes through the points (–4, 3) and (2, –6). If line q is generated by reflecting m across the line y = x, then which of the following represents the equation of q?
3x + 2y = 6
3x + 2y = 18
2x + 3y = –6
2x + 3y = 6
–2x + 3y = 6
Explanation
When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a).
Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2).
Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.
First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x1, y1) and (x2, y2).
slope = (2 – (–4))/(–6 –3)
= 6/–9 = –2/3
Next, we can use the point-slope formula to find the equation for q.
y – y1 = slope(x – x1)
y – 2 = (–2/3)(x – (–6))
Multiply both sides by 3.
3(y – 2) = –2(x + 6)
3y – 6 = –2x – 12
Add 2x to both sides.
2x + 3y – 6 = –12
Add six to both sides.
2x + 3y = –6
The answer is 2x + 3y = –6.
Line m passes through the points (–4, 3) and (2, –6). If line q is generated by reflecting m across the line y = x, then which of the following represents the equation of q?
3x + 2y = 6
3x + 2y = 18
2x + 3y = –6
2x + 3y = 6
–2x + 3y = 6
Explanation
When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a).
Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2).
Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.
First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x1, y1) and (x2, y2).
slope = (2 – (–4))/(–6 –3)
= 6/–9 = –2/3
Next, we can use the point-slope formula to find the equation for q.
y – y1 = slope(x – x1)
y – 2 = (–2/3)(x – (–6))
Multiply both sides by 3.
3(y – 2) = –2(x + 6)
3y – 6 = –2x – 12
Add 2x to both sides.
2x + 3y – 6 = –12
Add six to both sides.
2x + 3y = –6
The answer is 2x + 3y = –6.
Bobby draws a circle on graph paper with a center at (2, 5) and a radius of 10.
Jenny moves Bobby's circle up 2 units and to the right 1 unit.
What is the equation of Jenny's circle?
Explanation
If Jenny moves Bobby's circle up 2 units and to the right 1 unit, then the center of her circle is (3, 7). The radius remains 10.
The general equation for a circle with center (h, k) and radius r is given by
For Jenny's circle, (h, k) = (3, 7) and r=10.
Substituting these values into the general equation gives us
Bobby draws a circle on graph paper with a center at (2, 5) and a radius of 10.
Jenny moves Bobby's circle up 2 units and to the right 1 unit.
What is the equation of Jenny's circle?
Explanation
If Jenny moves Bobby's circle up 2 units and to the right 1 unit, then the center of her circle is (3, 7). The radius remains 10.
The general equation for a circle with center (h, k) and radius r is given by
For Jenny's circle, (h, k) = (3, 7) and r=10.
Substituting these values into the general equation gives us
Let f(x) = x3 – 2x2 + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?
–x3 – 2x2 – x – 4
–x3 + 2x2 – x + 4
x3 + 2x2 + x + 4
–x3 – 2x2 – x + 4
x3 – 2x2 – x + 4
Explanation
In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.

Therefore, g(x) = f(–x).
f(x) = x3 – 2x2 + x – 4
g(x) = f(–x) = (–x)3 – 2(–x)2 + (–x) + 4
g(x) = (–1)3x3 –2(–1)2x2 – x + 4
g(x) = –x3 –2x2 –x + 4.
The answer is –x3 –2x2 –x + 4.
Let f(x) = x3 – 2x2 + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?
–x3 – 2x2 – x – 4
–x3 + 2x2 – x + 4
x3 + 2x2 + x + 4
–x3 – 2x2 – x + 4
x3 – 2x2 – x + 4
Explanation
In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.

Therefore, g(x) = f(–x).
f(x) = x3 – 2x2 + x – 4
g(x) = f(–x) = (–x)3 – 2(–x)2 + (–x) + 4
g(x) = (–1)3x3 –2(–1)2x2 – x + 4
g(x) = –x3 –2x2 –x + 4.
The answer is –x3 –2x2 –x + 4.
The following is an equation of a circle:
If this circle is moved to the left 2 spaces and down 3 spaces, where does the center of the new circle lie?
Explanation
The general formula for a circle with center (h,k) and radius r is 
The center of the original circle, therefore, is (2, -4).
If we move the circle to the left 2 spaces and down 3 spaces, then the center of the new circle is given by 

The following is an equation of a circle:
If this circle is moved to the left 2 spaces and down 3 spaces, where does the center of the new circle lie?
Explanation
The general formula for a circle with center (h,k) and radius r is 
The center of the original circle, therefore, is (2, -4).
If we move the circle to the left 2 spaces and down 3 spaces, then the center of the new circle is given by 

The graphs of 



Explanation
Let f(x) = -2x2 + 3x - 5. If g(x) represents f(x) after it has been shifted to the left by three units, and then shifted down by four, which of the following is equal to g(x)?
-2x^2 + 3x - 12
-2x^2 + 15x - 36
-2x^2 + 31x - 124
-2x^2 - 9x - 18
-2x^2 - 9
Explanation
We are told that g(x) is found by taking f(x) and shifting it to the left by three and then down by four. This means that we can represent g(x) as follows:
g(x) = f(x + 3) - 4
Remember that the function f(x + 3) represents f(x) after it has been shifted to the LEFT by three, whereas f(x - 3) represents f(x) after being shifted to the RIGHT by three.
f(x) = -2x2 + 3x - 5
g(x) = f(x + 3) - 4 = \[-2(x+3)2 + 3(x+3) - 5\] - 4
g(x) = -2(x2 + 6x + 9) + 3x + 9 - 5 - 4
g(x) = -2x2 -12x -18 + 3x + 9 - 5 - 4
g(x) = -2x2 - 9x - 18 + 9 - 5 - 4
g(x) = -2x2 - 9x - 18
The answer is -2x2 - 9x - 18.