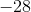Absolute Value
Help Questions
SAT Math › Absolute Value
Which of the following sentences is represented by the equation
The absolute value of the sum of a number and seven is three less than the number.
The absolute value of the sum of a number and seven is three greater than the number.
The sum of three and the absolute value of the sum of a number is three greater than the number.
The sum of three and the absolute value of the sum of a number is three less than the number.
None of the other responses are correct.
Explanation




"The absolute value of the sum of a number and seven is three less than the number."
Let 




Explanation
We need to solve the two equations |2a – 3| = 5 and |3 – 4b| = 11, in order to determine the possible values of a and b. When solving equations involving absolute values, we must remember to consider both the positive and negative cases. For example, if |x| = 4, then x can be either 4 or –4.
Let's look at |2a – 3| = 5. The two equations we need to solve are 2a – 3 = 5 and 2a – 3 = –5.
2a – 3 = 5 or 2a – 3 = –5
Add 3 to both sides.
2a = 8 or 2a = –2
Divide by 2.
a = 4 or a = –1
Therefore, the two possible values for a are 4 and –1. However, the problem states that both a and b are negative. Thus, a must equal –1.
Let's now find the values of b.
3 – 4b = 11 or 3 – 4b = –11
Subtract 3 from both sides.
–4b = 8 or –4b = –14
Divide by –4.
b = –2 or b = 7/2
Since b must also be negative, b must equal –2.
We have determined that a is –1 and b is –2. The original question asks us to find |b – a|.
|b – a| = |–2 – (–1)| = | –2 + 1 | = |–1| = 1.
The answer is 1.
Let 




Explanation
We need to solve the two equations |2a – 3| = 5 and |3 – 4b| = 11, in order to determine the possible values of a and b. When solving equations involving absolute values, we must remember to consider both the positive and negative cases. For example, if |x| = 4, then x can be either 4 or –4.
Let's look at |2a – 3| = 5. The two equations we need to solve are 2a – 3 = 5 and 2a – 3 = –5.
2a – 3 = 5 or 2a – 3 = –5
Add 3 to both sides.
2a = 8 or 2a = –2
Divide by 2.
a = 4 or a = –1
Therefore, the two possible values for a are 4 and –1. However, the problem states that both a and b are negative. Thus, a must equal –1.
Let's now find the values of b.
3 – 4b = 11 or 3 – 4b = –11
Subtract 3 from both sides.
–4b = 8 or –4b = –14
Divide by –4.
b = –2 or b = 7/2
Since b must also be negative, b must equal –2.
We have determined that a is –1 and b is –2. The original question asks us to find |b – a|.
|b – a| = |–2 – (–1)| = | –2 + 1 | = |–1| = 1.
The answer is 1.
Which of the following sentences is represented by the equation
The absolute value of the sum of a number and seven is three less than the number.
The absolute value of the sum of a number and seven is three greater than the number.
The sum of three and the absolute value of the sum of a number is three greater than the number.
The sum of three and the absolute value of the sum of a number is three less than the number.
None of the other responses are correct.
Explanation




"The absolute value of the sum of a number and seven is three less than the number."
Evaluate for 
Explanation
Substitute 0.6 for 
Evaluate for 
Explanation
Substitute 0.6 for 
If 

Explanation
Substitute – 4 in for x. Remember that when a negative number is raised to the third power, it is negative. - = – 64. – 64 – 36 = – 100. Since you are asked to take the absolute value of – 100 the final value of f(-4) = 100. The absolute value of any number is positive.
If 

Explanation
Substitute – 4 in for x. Remember that when a negative number is raised to the third power, it is negative. - = – 64. – 64 – 36 = – 100. Since you are asked to take the absolute value of – 100 the final value of f(-4) = 100. The absolute value of any number is positive.
Define an operation 
For all real numbers 
Evaluate: 
The expression is undefined.
None of the other responses is correct.
Explanation

Define an operation 
For all real numbers 
Evaluate: 
The expression is undefined.
None of the other responses is correct.
Explanation