Variables - SAT Math
Card 0 of 480
Subtract  from
from  .
.
Subtract 

Step 1: We need to read the question carefully. It says subtract from. When you see the word "from", you read the question right to left.
I am subtracting the left equation from the right equation.
Step 2: We need to write the equation on the right minus the equation of the left.

Step 3: Distribute the minus sign in front of the parentheses:

Step 4: Combine like terms:



Step 5: Put all the terms together, starting with highest degree. The degree of the terms is the exponent. Here, the highest degree is 2 and lowest is zero.
The final equation is 
Step 1: We need to read the question carefully. It says subtract from. When you see the word "from", you read the question right to left.
I am subtracting the left equation from the right equation.
Step 2: We need to write the equation on the right minus the equation of the left.
Step 3: Distribute the minus sign in front of the parentheses:
Step 4: Combine like terms:
Step 5: Put all the terms together, starting with highest degree. The degree of the terms is the exponent. Here, the highest degree is 2 and lowest is zero.
The final equation is
Compare your answer with the correct one above
Define an operation  on the set of real numbers as follows:
on the set of real numbers as follows:
For all real  ,
,

How else could this operation be defined?
Define an operation 
For all real 
How else could this operation be defined?
 , as the cube of a binomial, can be rewritten using the following pattern:
, as the cube of a binomial, can be rewritten using the following pattern:

Applying the rules of exponents to simplify this:
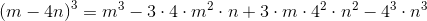

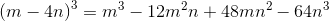
Therefore, the correct choice is that, alternatively stated,
 .
.

Applying the rules of exponents to simplify this:
Therefore, the correct choice is that, alternatively stated,

Compare your answer with the correct one above
Phillip can paint  square feet of wall per minute. What area of the wall can he paint in 2.5 hours?
square feet of wall per minute. What area of the wall can he paint in 2.5 hours?
Phillip can paint 
Every minute Phillip completes another _ square feet of painting. To solve for the total area that he completes, we need to find the number of minutes that he works.
square feet of painting. To solve for the total area that he completes, we need to find the number of minutes that he works.
There are 60 minutes in an hour, and he paints for 2.5 hours. Multiply to find the total number of minutes.

If he completes _ square feet per minute, then we can multiply _
square feet per minute, then we can multiply _ by the total minutes to find the final answer.
by the total minutes to find the final answer.

Every minute Phillip completes another _
There are 60 minutes in an hour, and he paints for 2.5 hours. Multiply to find the total number of minutes.
If he completes _

Compare your answer with the correct one above
The value of  varies directly with the square of _
varies directly with the square of _ _and the cube of
_and the cube of  . If
. If  when
when  and
and  , then what is the value of _
, then what is the value of _ when
when  and
and  ?
?
The value of 








Let's consider the general case when y varies directly with x. If y varies directly with x, then we can express their relationship to one another using the following formula:
y = kx, where k is a constant.
Therefore, if y varies directly as the square of x and the cube of z, we can write the following analagous equation:
y = _kx_2_z_3, where k is a constant.
The problem states that y = 24 when x = 1 and z = 2. We can use this information to solve for k by substituting the known values for y, x, and z.
24 = k(1)2(2)3 = k(1)(8) = 8_k_
24 = 8_k_
Divide both sides by 8.
3 = k
k = 3
Now that we have k, we can find y if we know x and z. The problem asks us to find y when x = 3 and z = 1. We will use our formula for direct variation again, this time substitute values for k, x, and z.
y = _kx_2_z_3
y = 3(3)2(1)3 = 3(9)(1) = 27
y = 27
The answer is 27.
Let's consider the general case when y varies directly with x. If y varies directly with x, then we can express their relationship to one another using the following formula:
y = kx, where k is a constant.
Therefore, if y varies directly as the square of x and the cube of z, we can write the following analagous equation:
y = _kx_2_z_3, where k is a constant.
The problem states that y = 24 when x = 1 and z = 2. We can use this information to solve for k by substituting the known values for y, x, and z.
24 = k(1)2(2)3 = k(1)(8) = 8_k_
24 = 8_k_
Divide both sides by 8.
3 = k
k = 3
Now that we have k, we can find y if we know x and z. The problem asks us to find y when x = 3 and z = 1. We will use our formula for direct variation again, this time substitute values for k, x, and z.
y = _kx_2_z_3
y = 3(3)2(1)3 = 3(9)(1) = 27
y = 27
The answer is 27.
Compare your answer with the correct one above
In a growth period, a population of flies triples every week. If the original population had 3 flies, how big is the population after 4 weeks?
In a growth period, a population of flies triples every week. If the original population had 3 flies, how big is the population after 4 weeks?
We know that the initial population is 3, and that every week the population will triple.
The equation to model this growth will be  , where
, where  is the initial size,
is the initial size,  is the rate of growth, and
is the rate of growth, and  is the time.
is the time.
In this case, the equation will be  .
.

Alternatively, you can evaluate for each consecutive week.
Week 1: 
Week 2: 
Week 3: 
Week 4: 
We know that the initial population is 3, and that every week the population will triple.
The equation to model this growth will be 



In this case, the equation will be 
Alternatively, you can evaluate for each consecutive week.
Week 1:
Week 2:
Week 3:
Week 4:
Compare your answer with the correct one above
 and
and  are the radius and volume, respectively, of a given sphere.
are the radius and volume, respectively, of a given sphere.

![W = \sqrt[3]{V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500721/gif.latex) .
.
Which of the following is a true statement?


![W = \sqrt[3]{V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500721/gif.latex)
Which of the following is a true statement?
The volume of a sphere can be calculated from its radius as follows:

Therefore, squaring both sides, we get



![W = \sqrt[3]{V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500726/gif.latex)
![W ^{6 }= \left (\sqrt[3]{V} \right ) ^{6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500727/gif.latex)

Substituting:




If we let the constant of variation be  , we see that
, we see that
 ,
,
and  varies directly as
varies directly as  , the sixth power of
, the sixth power of  .
.
The volume of a sphere can be calculated from its radius as follows:
Therefore, squaring both sides, we get
Substituting:
If we let the constant of variation be 

and 


Compare your answer with the correct one above
 and
and  are the diameter and circumference, respectively, of the same circle.
are the diameter and circumference, respectively, of the same circle.


Which of the following is a true statement? (Assume all quantities are positive)


Which of the following is a true statement? (Assume all quantities are positive)
If  and
and  are the diameter and circumference, respectively, of the same circle, then
are the diameter and circumference, respectively, of the same circle, then
 .
.
By substitution,


Taking the square root of both sides:



Taking  as the constant of variation, we get
as the constant of variation, we get
 ,
,
meaning that  varies directly as
varies directly as  .
.
If 


By substitution,
Taking the square root of both sides:
Taking 

meaning that 

Compare your answer with the correct one above
 is the radius of the base of a cone;
is the radius of the base of a cone;  is its height;
is its height;  is its volume.
is its volume.
 ;
;  .
.
Which of the following is a true statement?





Which of the following is a true statement?
The volume of a cone can be calculated from the radius of its base  , and the height
, and the height  , using the formula
, using the formula

 , so
, so  .
.
 , so
, so  .
.
 , so by substitution,
, so by substitution,



Square both sides:





If we take  as the constant of variation, then
as the constant of variation, then
 ,
,
and  varies directly as the fifth power of
varies directly as the fifth power of  .
.
The volume of a cone can be calculated from the radius of its base 






Square both sides:
If we take 

and 

Compare your answer with the correct one above
The temperature at the surface of the ocean is  . At
. At  meters below the surface, the ocean temperature is
meters below the surface, the ocean temperature is  . By how much does the temperature decrease for every
. By how much does the temperature decrease for every  meters below the ocean's surface?
meters below the ocean's surface?
The temperature at the surface of the ocean is 



This may seem confusing, but is pretty straightforward.







Thus, for every 125 meters below the surface, the temperature decreases by one degree.
To find how much it decreases with every 100 meters, we need to do the following:

Thus, the temperature decreases by  every 100 meters.
every 100 meters.
This may seem confusing, but is pretty straightforward.
Thus, for every 125 meters below the surface, the temperature decreases by one degree.
To find how much it decreases with every 100 meters, we need to do the following:
Thus, the temperature decreases by 
Compare your answer with the correct one above
Phillip can paint  square feet of wall per minute. What area of the wall can he paint in 2.5 hours?
square feet of wall per minute. What area of the wall can he paint in 2.5 hours?
Phillip can paint 
Every minute Phillip completes another _ square feet of painting. To solve for the total area that he completes, we need to find the number of minutes that he works.
square feet of painting. To solve for the total area that he completes, we need to find the number of minutes that he works.
There are 60 minutes in an hour, and he paints for 2.5 hours. Multiply to find the total number of minutes.

If he completes _ square feet per minute, then we can multiply _
square feet per minute, then we can multiply _ by the total minutes to find the final answer.
by the total minutes to find the final answer.

Every minute Phillip completes another _
There are 60 minutes in an hour, and he paints for 2.5 hours. Multiply to find the total number of minutes.
If he completes _

Compare your answer with the correct one above
The value of  varies directly with the square of _
varies directly with the square of _ _and the cube of
_and the cube of  . If
. If  when
when  and
and  , then what is the value of _
, then what is the value of _ when
when  and
and  ?
?
The value of 








Let's consider the general case when y varies directly with x. If y varies directly with x, then we can express their relationship to one another using the following formula:
y = kx, where k is a constant.
Therefore, if y varies directly as the square of x and the cube of z, we can write the following analagous equation:
y = _kx_2_z_3, where k is a constant.
The problem states that y = 24 when x = 1 and z = 2. We can use this information to solve for k by substituting the known values for y, x, and z.
24 = k(1)2(2)3 = k(1)(8) = 8_k_
24 = 8_k_
Divide both sides by 8.
3 = k
k = 3
Now that we have k, we can find y if we know x and z. The problem asks us to find y when x = 3 and z = 1. We will use our formula for direct variation again, this time substitute values for k, x, and z.
y = _kx_2_z_3
y = 3(3)2(1)3 = 3(9)(1) = 27
y = 27
The answer is 27.
Let's consider the general case when y varies directly with x. If y varies directly with x, then we can express their relationship to one another using the following formula:
y = kx, where k is a constant.
Therefore, if y varies directly as the square of x and the cube of z, we can write the following analagous equation:
y = _kx_2_z_3, where k is a constant.
The problem states that y = 24 when x = 1 and z = 2. We can use this information to solve for k by substituting the known values for y, x, and z.
24 = k(1)2(2)3 = k(1)(8) = 8_k_
24 = 8_k_
Divide both sides by 8.
3 = k
k = 3
Now that we have k, we can find y if we know x and z. The problem asks us to find y when x = 3 and z = 1. We will use our formula for direct variation again, this time substitute values for k, x, and z.
y = _kx_2_z_3
y = 3(3)2(1)3 = 3(9)(1) = 27
y = 27
The answer is 27.
Compare your answer with the correct one above
In a growth period, a population of flies triples every week. If the original population had 3 flies, how big is the population after 4 weeks?
In a growth period, a population of flies triples every week. If the original population had 3 flies, how big is the population after 4 weeks?
We know that the initial population is 3, and that every week the population will triple.
The equation to model this growth will be  , where
, where  is the initial size,
is the initial size,  is the rate of growth, and
is the rate of growth, and  is the time.
is the time.
In this case, the equation will be  .
.

Alternatively, you can evaluate for each consecutive week.
Week 1: 
Week 2: 
Week 3: 
Week 4: 
We know that the initial population is 3, and that every week the population will triple.
The equation to model this growth will be 



In this case, the equation will be 
Alternatively, you can evaluate for each consecutive week.
Week 1:
Week 2:
Week 3:
Week 4:
Compare your answer with the correct one above
 and
and  are the radius and volume, respectively, of a given sphere.
are the radius and volume, respectively, of a given sphere.

![W = \sqrt[3]{V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500721/gif.latex) .
.
Which of the following is a true statement?


![W = \sqrt[3]{V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500721/gif.latex)
Which of the following is a true statement?
The volume of a sphere can be calculated from its radius as follows:

Therefore, squaring both sides, we get



![W = \sqrt[3]{V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500726/gif.latex)
![W ^{6 }= \left (\sqrt[3]{V} \right ) ^{6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500727/gif.latex)

Substituting:




If we let the constant of variation be  , we see that
, we see that
 ,
,
and  varies directly as
varies directly as  , the sixth power of
, the sixth power of  .
.
The volume of a sphere can be calculated from its radius as follows:
Therefore, squaring both sides, we get
Substituting:
If we let the constant of variation be 

and 


Compare your answer with the correct one above
 and
and  are the diameter and circumference, respectively, of the same circle.
are the diameter and circumference, respectively, of the same circle.


Which of the following is a true statement? (Assume all quantities are positive)


Which of the following is a true statement? (Assume all quantities are positive)
If  and
and  are the diameter and circumference, respectively, of the same circle, then
are the diameter and circumference, respectively, of the same circle, then
 .
.
By substitution,


Taking the square root of both sides:



Taking  as the constant of variation, we get
as the constant of variation, we get
 ,
,
meaning that  varies directly as
varies directly as  .
.
If 


By substitution,
Taking the square root of both sides:
Taking 

meaning that 

Compare your answer with the correct one above
 is the radius of the base of a cone;
is the radius of the base of a cone;  is its height;
is its height;  is its volume.
is its volume.
 ;
;  .
.
Which of the following is a true statement?





Which of the following is a true statement?
The volume of a cone can be calculated from the radius of its base  , and the height
, and the height  , using the formula
, using the formula

 , so
, so  .
.
 , so
, so  .
.
 , so by substitution,
, so by substitution,



Square both sides:





If we take  as the constant of variation, then
as the constant of variation, then
 ,
,
and  varies directly as the fifth power of
varies directly as the fifth power of  .
.
The volume of a cone can be calculated from the radius of its base 






Square both sides:
If we take 

and 

Compare your answer with the correct one above
The temperature at the surface of the ocean is  . At
. At  meters below the surface, the ocean temperature is
meters below the surface, the ocean temperature is  . By how much does the temperature decrease for every
. By how much does the temperature decrease for every  meters below the ocean's surface?
meters below the ocean's surface?
The temperature at the surface of the ocean is 



This may seem confusing, but is pretty straightforward.







Thus, for every 125 meters below the surface, the temperature decreases by one degree.
To find how much it decreases with every 100 meters, we need to do the following:

Thus, the temperature decreases by  every 100 meters.
every 100 meters.
This may seem confusing, but is pretty straightforward.
Thus, for every 125 meters below the surface, the temperature decreases by one degree.
To find how much it decreases with every 100 meters, we need to do the following:
Thus, the temperature decreases by 
Compare your answer with the correct one above
Factor the following variable
(x2 + 18x + 72)
Factor the following variable
(x2 + 18x + 72)
You need to find two numbers that multiply to give 72 and add up to give 18
easiest way: write the multiples of 72:
1, 72
2, 36
3, 24
4, 18
6, 12: these add up to 18
(x + 6)(x + 12)
You need to find two numbers that multiply to give 72 and add up to give 18
easiest way: write the multiples of 72:
1, 72
2, 36
3, 24
4, 18
6, 12: these add up to 18
(x + 6)(x + 12)
Compare your answer with the correct one above
When  is factored, it can be written in the form
is factored, it can be written in the form  , where
, where  ,
,  ,
,  ,
,  ,
,  , and
, and  are all integer constants, and
are all integer constants, and  .
.
What is the value of  ?
?
When 








What is the value of 
Let's try to factor x2 – y2 – z2 + 2yz.
Notice that the last three terms are very close to y2 + z2 – 2yz, which, if we rearranged them, would become y2 – 2yz+ z2. We could factor y2 – 2yz+ z2 as (y – z)2, using the general rule that p2 – 2pq + q2 = (p – q)2 .
So we want to rearrange the last three terms. Let's group them together first.
x2 + (–y2 – z2 + 2yz)
If we were to factor out a –1 from the last three terms, we would have the following:
x2 – (y2 + z2 – 2yz)
Now we can replace y2 + z2 – 2yz with (y – z)2.
x2 – (y – z)2
This expression is actually a differences of squares. In general, we can factor p2 – q2 as (p – q)(p + q). In this case, we can substitute x for p and (y – z) for q.
x2 – (y – z)2 = (x – (y – z))(x + (y – z))
Now, let's distribute the negative one in the trinomial x – (y – z)
(x – (y – z))(x + (y – z))
(x – y + z)(x + y – z)
The problem said that factoring x2 – y2 – z2 + 2yz would result in two polynomials in the form (ax + by + cz)(dx + ey + fz), where a, b, c, d, e, and f were all integers, and a > 0.
(x – y + z)(x + y – z) fits this form. This means that a = 1, b = –1, c = 1, d = 1, e = 1, and f = –1. The sum of all of these is 2.
The answer is 2.
Let's try to factor x2 – y2 – z2 + 2yz.
Notice that the last three terms are very close to y2 + z2 – 2yz, which, if we rearranged them, would become y2 – 2yz+ z2. We could factor y2 – 2yz+ z2 as (y – z)2, using the general rule that p2 – 2pq + q2 = (p – q)2 .
So we want to rearrange the last three terms. Let's group them together first.
x2 + (–y2 – z2 + 2yz)
If we were to factor out a –1 from the last three terms, we would have the following:
x2 – (y2 + z2 – 2yz)
Now we can replace y2 + z2 – 2yz with (y – z)2.
x2 – (y – z)2
This expression is actually a differences of squares. In general, we can factor p2 – q2 as (p – q)(p + q). In this case, we can substitute x for p and (y – z) for q.
x2 – (y – z)2 = (x – (y – z))(x + (y – z))
Now, let's distribute the negative one in the trinomial x – (y – z)
(x – (y – z))(x + (y – z))
(x – y + z)(x + y – z)
The problem said that factoring x2 – y2 – z2 + 2yz would result in two polynomials in the form (ax + by + cz)(dx + ey + fz), where a, b, c, d, e, and f were all integers, and a > 0.
(x – y + z)(x + y – z) fits this form. This means that a = 1, b = –1, c = 1, d = 1, e = 1, and f = –1. The sum of all of these is 2.
The answer is 2.
Compare your answer with the correct one above
Factor 9_x_2 + 12_x_ + 4.
Factor 9_x_2 + 12_x_ + 4.
Nothing common cancels at the beginning. To factor this, we need to find two numbers that multiply to 9 * 4 = 36 and sum to 12. 6 and 6 work.
So 9_x_2 + 12_x_ + 4 = 9_x_2 + 6_x_ + 6_x_ + 4
Let's look at the first two terms and last two terms separately to begin with. 9_x_2 + 6_x_ can be simplified to 3_x_(3_x_ + 2) and 6_x_ + 4 can be simplified into 2(3_x_ + 2). Putting these together gets us
9_x_2 + 12_x_ + 4
= 9_x_2 + 6_x_ + 6_x_ + 4
= 3_x_(3_x_ + 2) + 2(3_x_ + 2)
= (3_x_ + 2)(3_x_ + 2)
This is as far as we can factor.
Nothing common cancels at the beginning. To factor this, we need to find two numbers that multiply to 9 * 4 = 36 and sum to 12. 6 and 6 work.
So 9_x_2 + 12_x_ + 4 = 9_x_2 + 6_x_ + 6_x_ + 4
Let's look at the first two terms and last two terms separately to begin with. 9_x_2 + 6_x_ can be simplified to 3_x_(3_x_ + 2) and 6_x_ + 4 can be simplified into 2(3_x_ + 2). Putting these together gets us
9_x_2 + 12_x_ + 4
= 9_x_2 + 6_x_ + 6_x_ + 4
= 3_x_(3_x_ + 2) + 2(3_x_ + 2)
= (3_x_ + 2)(3_x_ + 2)
This is as far as we can factor.
Compare your answer with the correct one above
Factor and simplify:

Factor and simplify:
 is a difference of squares.
is a difference of squares.
The difference of squares formula is  .
.
Therefore,  =
=  .
.

The difference of squares formula is 
Therefore, 

Compare your answer with the correct one above