Triangles - SAT Math

Card 0 of 1184

Question

Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?

Answer

The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.

Compare your answer with the correct one above

Question

If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?

Answer

According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.

Compare your answer with the correct one above

Question

A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?

Answer

The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.

Compare your answer with the correct one above

Question

Two sides of a triangle are 20 and 32. Which of the following CANNOT be the third side of this triangle.

Answer

Please remember the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Therefore, the correct answer is 10 because the sum of 10 and 20 would not be greater than the third side 32.

Compare your answer with the correct one above

Question

A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?

Answer

The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.

Compare your answer with the correct one above

Question

The lengths of two sides of a triangle are 9 and 7. Which of the following could be the length of the third side?

Answer

Let us call the third side x. According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be larger than the other two sides. Thus, all of the following must be true:

x + 7 > 9

x + 9 > 7

7 + 9 > x

We can solve these three inequalities to determine the possible values of x.

x + 7 > 9

Subtract 7 from both sides.

x > 2

Now, we can look at x + 9 > 7. Subtracting 9 from both sides, we obtain

x > –2

Finally, 7 + 9 > x, which means that 16 > x.

Therefore, x must be greater than 2, greater than –2, but also less than 16. The only number that satisfies all of these requirements is 12.

The answer is 12.

Compare your answer with the correct one above

Question

The lengths of a triangle are 8, 12, and x. Which of the following inequalities shows all of the possible values of x?

Answer

According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater (not greater than or equal) than the remaining side. Thus, the following inequalities must all be true:

x + 8 > 12

x + 12 > 8

8 + 12 > x

Let's solve each inequality.

x + 8 > 12

Subtract 8 from both sides.

x > 4

Next, let's look at the inequality x + 12 > 8

x + 12 > 8

Subtract 12 from both sides.

x > –4

Lastly, 8 + 12 > x, which means that x < 20.

This means that x must be less than twenty, but greater than 4 and greater than –4. Since any number greater than 4 is also greater than –4, we can exclude the inequality x > –4.

To summarize, x must be greater than 4 and less than 20. We can write this as 4 < x < 20.

The answer is 4 < x < 20.

Compare your answer with the correct one above

Question

If 2 sides of the triangle are have lengths equal to 8 and 14, what is one possible length of the third side?

Answer

The sum of the lengths of 2 sides of a triangle must be greater than—but not equal to—the length of the third side. Further, the third side must be longer than the difference between the greater and the lesser of the other two sides; therefore, 20 is the only possible answer.

$4+8< 14$

$6+8= 14$

$8+14> 20$

$8+14=22$

Compare your answer with the correct one above

Question

In $\Delta ABC$ the length of AB is 15 and the length of side AC is 5. What is the least possible integer length of side BC?

Answer

Rule - the length of one side of a triangle must be greater than the differnce and less than the sum of the lengths of the other two sides.

Given lengths of two of the sides of the $\Delta ABC$ are 15 and 5. The length of the third side must be greater than 15-5 or 10 and less than 15+5 or 20.

The question asks what is the least possible integer length of BC, which would be 11

Compare your answer with the correct one above

Question

Given $\bigtriangleup ABC$ with $m \angle A > m \angle B$ and $m \angle C = 60^{\circ }$ .

Which of the following could be the correct ordering of the lengths of the sides of the triangle?

I)

II)

III)

Answer

Given two angles of unequal measure in a triangle, the side opposite the greater angle is longer than the side opposite the other angle. Therefore, we seek to find the relationship among the measures of the angles.

$m \angle C = 60^{\circ }$ , and the measures of the interior angles of a triangle total $180^{\circ }$ , so

$m \angle A + m \angle B + m \angle C = 180 ^{\circ }$

$m \angle A + m \angle B + 60 ^{\circ } = 180 ^{\circ }$

$m \angle A + m \angle B = 120 ^{\circ }$

Since $m \angle A > m \angle B$ ,

$m \angle A + m \angle A > m \angle B+ m \angle A = 120^{\circ }$

$2 m \angle A > 120^{\circ }$

$m \angle A > 60^{\circ }$ ,

and, similarly,

$m \angle B < 60^{\circ }$

Therefore,

$m \angle A > m \angle C > m \angle B$ ,

and the lengths of their opposite sides rank similarly:

.

The correct response is that only (II) can be true.

Compare your answer with the correct one above

Question

Given $\bigtriangleup ABC$ with $m \angle A > m \angle B$ and $m \angle C = 45^{\circ }$ .

Which of the following could be the correct ordering of the lengths of the sides of the triangle?

I)

II)

III)

Answer

Given two angles of unequal measure in a triangle, the side opposite the greater angle is longer than the side opposite the other angle.

If $\angle C$ were the angle of greatest measure, then $m \angle A , m \angle B < 45^{\circ }$ , and

$m \angle A + m \angle B + m \angle C < 45 ^{\circ}+ 45 ^{\circ}+ 45 ^{\circ} = 135 ^{\circ} < 180 ^{\circ}$ .

Since the measures of the angles must total $180 ^{\circ}$ , $\angle C$ cannot have the greatest measure.

$m \angle A > m \angle B$ , so we can explore two other possibilities:

$m \angle A > m \angle B > m \angle C$ , which here is possible if, for example,

$m \angle A = 85 ^{\circ }$ and $m \angle B = 50 ^{\circ }$ - since ; and,

$m \angle A > m \angle C > m \angle B$ , which here is possible if, for example,

$m \angle A = 95 ^{\circ }$ and $m \angle B = 40 ^{\circ }$ - since .

If $m \angle A > m \angle B > m \angle C$ , then ; if $m \angle A > m \angle C > m \angle B$ , then .

This makes the correct response II or III only.

Compare your answer with the correct one above

Question

Which of the given answers choices could NOT represent the sides of a triangle?

Answer

In order for three lengths to represent the sides of a triangle, they must pass the Triangle Inequality.

This means that the sum of any two sides of the triangle must exceed the length of the third side.

With the given answers, the one set of lengths that fail this test is .

$4+5 \ngtr 10$

Therefore, the lengths could not represent the sides of a triangle.

Compare your answer with the correct one above

Question

A triangle with two equal angles is called a(n) .

Answer

An isoceles triangle is a triangle that has at least two congruent sides (and therefore, at least two congruent angles as well).

Compare your answer with the correct one above

Question

Find the height of a triangle if the area of the triangle = 18 and the base = 4.

Answer

The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.

Compare your answer with the correct one above

Question

In the figure above, line segments DC and AB are parallel. What is the perimeter of quadrilateral ABCD?

Answer

Because DC and AB are parallel, this means that angles CDB and ABD are equal. When two parallel lines are cut by a transversal line, alternate interior angles (such as CDB and ABD) are congruent.

Now, we can show that triangles ABD and BDC are similar. Both ABD and BDC are right triangles. This means that they have one angle that is the same—their right angle. Also, we just established that angles CDB and ABD are congruent. By the angle-angle similarity theorem, if two triangles have two angles that are congruent, they are similar. Thus triangles ABD and BDC are similar triangles.

We can use the similarity between triangles ABD and BDC to find the lengths of BC and CD. The length of BC is proportional to the length of AD, and the length of CD is proportional to the length of DB, because these sides correspond.

We don’t know the length of DB, but we can find it using the Pythagorean Theorem. Let a, b, and c represent the lengths of AD, AB, and BD respectively. According to the Pythagorean Theorem:

_a_2 + _b_2 = _c_2

152 + 202 = _c_2

625 = _c_2

c = 25

The length of BD is 25.

We now have what we need to find the perimeter of the quadrilateral.

Perimeter = sum of the lengths of AB, BC, CD, and DA.

Perimeter = 20 + 18.75 + 31.25 + 15 = 85

The answer is 85.

Compare your answer with the correct one above

Question

A traffic light hangs t feet from the ground, over a street. A man standing the shadow of the traffic light is h feet tall, and his shadow is s feet long. How far is the man standing from the spot on the street directly under the traffic light?

Answer

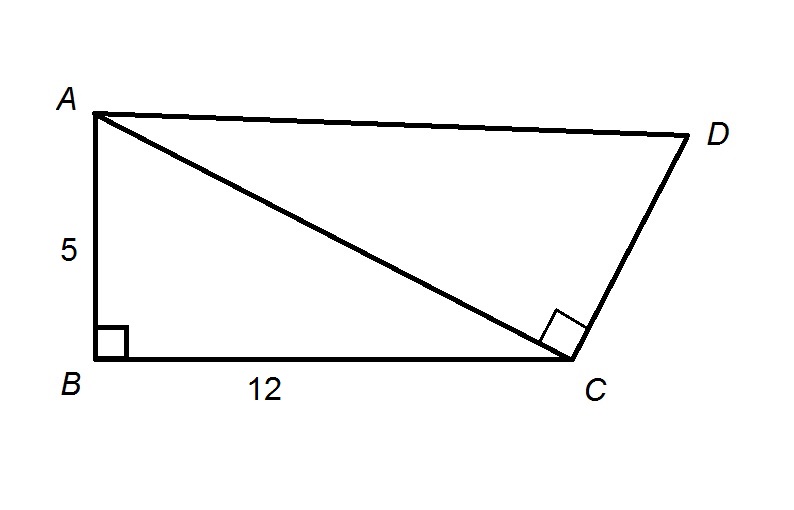
We can set this problem up like a set of similar triangles.

The first triangle is created by the three points: The Traffic light, the spot beneath the traffic light, and the spot where the man is standing (which is also the spot where the traffic light's shadow is).

The height of this Triangle is "T" as given in the question, and its base is the part that we are asked to solve for.

The second triangle is created by the top of the man's head, his feet, and the end of his shadow.

The height of this Triangle is "h" as given in the questions, and the base is "s".

We set up a proportion:

$\frac{height}{base} = \frac {T}{X} = \frac{h}{s}$

where X is the distance we are asked to find. Simply cross-multiply to solve.

$X = \frac{sT}{h}$

Compare your answer with the correct one above

Question

In the given diagram, $\bigtriangleup ABC \sim \bigtriangleup DCA$ . Give the area of $\bigtriangleup DCA$ to the nearest whole number.

Answer

By the Pythagorean Theorem,

$(AC)^{2}= (AB)^{2} + (BC)^{2}$

Set , and solve for :

$(AC)^{2}= (AB)^{2} + (BC)^{2}$

$(AC)^{2}= 5^{2} + 12^{2}$

$(AC)^{2}= 25+144$

$(AC)^{2}=169$

Take the positive square root of both sides:

$AC = \sqrt{169} = 13$

$\bigtriangleup ABC \sim \bigtriangleup DCA$ , so corresponding sides are in proportion; specifically,

$\frac{DC}{AB} = \frac{AC}{CB}$

Set , and solve for :

$\frac{DC}{5} = \frac{13}{12}$

$\frac{DC}{5} \cdot 5 = \frac{13}{12} \cdot 5$

$DC = \frac{65}{12} = 5 \frac{5}{12}$

A right triangle has as its area half the product of the length of its legs, so the area of $\bigtriangleup DCA$ is

$\frac{1}{2} \cdot AC \cdot DC$

$= \frac{1}{2} \cdot 13 \cdot 5 \frac{5}{12}$

$= 35 \frac{5}{24}$

To the nearest whole number, this rounds to 35.

Compare your answer with the correct one above

Question

An meteor crashed in the desert and created an oblong shaped crater. Scientists want to find the width of the crater as it is near their research facility. Line segments AC and DE intersect at B making the angles E and D the same. If AB is 2000 meters, BD is 1800 meters, DC is 600 meters and EB is 3600 meters, what is the width of the crater?

Answer

To calculate the width of the crater, use the given information to establish that the image draws similar triangles. When triangles that have corresponding angles and a ratio to their side lengths they are considered to be similar triangles.

Identify the known information.

$\ \angle E=\angle D \\angle B=\angle B$

therefore,

$\angle A=\angle C$

and the bases of the triangles are parallel.

Also,

$\\overline{AB}=1800 \text{ m} \\overline{EB}=3600\text{ m} \\overline{BD}=1800 \text{ m} \\overline{CD}=600\text{ m}$

Set up the side ratios for this particular problem.

$\frac{AB}{BC}; \frac{AE}{CD}; \frac{EB}{BD}$

$\frac{1800}{BC}; \frac{x}{600}; \frac{3600}{1800}$

Looking at the only full ratio that is given, the scalar multiplier can be found.

$\frac{3600}{1800}=2$

Therefore, to find the width of the crater multiply $\overline{CD}$ by two.

$\\frac{x}{600}=2 \\x=2\cdot 600 \x=1200\text{ m}$

Compare your answer with the correct one above

Question

In the figure above, line segments DC and AB are parallel. What is the perimeter of quadrilateral ABCD?

Answer

Because DC and AB are parallel, this means that angles CDB and ABD are equal. When two parallel lines are cut by a transversal line, alternate interior angles (such as CDB and ABD) are congruent.

Now, we can show that triangles ABD and BDC are similar. Both ABD and BDC are right triangles. This means that they have one angle that is the same—their right angle. Also, we just established that angles CDB and ABD are congruent. By the angle-angle similarity theorem, if two triangles have two angles that are congruent, they are similar. Thus triangles ABD and BDC are similar triangles.

We can use the similarity between triangles ABD and BDC to find the lengths of BC and CD. The length of BC is proportional to the length of AD, and the length of CD is proportional to the length of DB, because these sides correspond.

We don’t know the length of DB, but we can find it using the Pythagorean Theorem. Let a, b, and c represent the lengths of AD, AB, and BD respectively. According to the Pythagorean Theorem:

_a_2 + _b_2 = _c_2

152 + 202 = _c_2

625 = _c_2

c = 25

The length of BD is 25.

We now have what we need to find the perimeter of the quadrilateral.

Perimeter = sum of the lengths of AB, BC, CD, and DA.

Perimeter = 20 + 18.75 + 31.25 + 15 = 85

The answer is 85.

Compare your answer with the correct one above

Question

A traffic light hangs t feet from the ground, over a street. A man standing the shadow of the traffic light is h feet tall, and his shadow is s feet long. How far is the man standing from the spot on the street directly under the traffic light?

Answer

We can set this problem up like a set of similar triangles.

The first triangle is created by the three points: The Traffic light, the spot beneath the traffic light, and the spot where the man is standing (which is also the spot where the traffic light's shadow is).

The height of this Triangle is "T" as given in the question, and its base is the part that we are asked to solve for.

The second triangle is created by the top of the man's head, his feet, and the end of his shadow.

The height of this Triangle is "h" as given in the questions, and the base is "s".

We set up a proportion:

$\frac{height}{base} = \frac {T}{X} = \frac{h}{s}$

where X is the distance we are asked to find. Simply cross-multiply to solve.

$X = \frac{sT}{h}$

Compare your answer with the correct one above

Tap the card to reveal the answer