New SAT Math - No Calculator - SAT Math
Card 0 of 366
If  , then
, then 
If 
 ,
,


Compare your answer with the correct one above
If  , what is the value of
, what is the value of  ?
?
If 

Compare your answer with the correct one above
If  , what does
, what does  equal?
equal?
If 

Subtract  and
and  from the both sides to get
from the both sides to get  .
.
Divide both sides by  , to get
, to get

Subtract 


Divide both sides by 
Compare your answer with the correct one above
 and
and  are similar triangles. The perimeter of Triangle A is 45” and the length of two of its sides are 15” and 10”. If the perimeter of Triangle B is 135” and what are lengths of two of its sides?
are similar triangles. The perimeter of Triangle A is 45” and the length of two of its sides are 15” and 10”. If the perimeter of Triangle B is 135” and what are lengths of two of its sides?


The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is 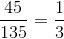 .
.
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“

The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is 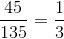
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“

Compare your answer with the correct one above
Which of the following lines is parallel to:

Which of the following lines is parallel to:
First write the equation in slope intercept form. Add  to both sides to get
to both sides to get  . Now divide both sides by
. Now divide both sides by  to get
to get  . The slope of this line is
. The slope of this line is  , so any line that also has a slope of
, so any line that also has a slope of  would be parallel to it. The correct answer is
would be parallel to it. The correct answer is  .
.
First write the equation in slope intercept form. Add 






Compare your answer with the correct one above


What is  ?
?
What is 
Solve for  by merging the equations so that
by merging the equations so that  gets factored out. To do so, multiply the lower equation by
gets factored out. To do so, multiply the lower equation by  (so that
(so that  at the top is subtracted by
at the top is subtracted by  )
)





Solve for 




Compare your answer with the correct one above
If

and

What is  ?
?
If
and
What is 
First, solve this equation for y and then substitute the answer into the second equation:

Now substitute into the second equation and solve for x:

To solve for x, add the coefficients on the x variables together then divide both sides by three.

First, solve this equation for y and then substitute the answer into the second equation:
Now substitute into the second equation and solve for x:
To solve for x, add the coefficients on the x variables together then divide both sides by three.
Compare your answer with the correct one above
A rectangular garden has an area of  . Its length is
. Its length is  meters longer than its width. How much fencing is needed to enclose the garden?
meters longer than its width. How much fencing is needed to enclose the garden?
A rectangular garden has an area of 

We define the variables as  and
and  .
.
We substitute these values into the equation for the area of a rectangle and get  .
.


 or
or 
Lengths cannot be negative, so the only correct answer is  . If
. If  , then
, then  .
.
Therefore,  .
.
We define the variables as 

We substitute these values into the equation for the area of a rectangle and get 

Lengths cannot be negative, so the only correct answer is 


Therefore, 
Compare your answer with the correct one above
Sally spent \$5.75 on pens and pencils for school. Each pencil cost 25 cents, and each pen cost 50 cents. If the number of pens Sally bought is one more than the number of pencils she bought, how many pencils and pens did she buy altogether?
Sally spent \$5.75 on pens and pencils for school. Each pencil cost 25 cents, and each pen cost 50 cents. If the number of pens Sally bought is one more than the number of pencils she bought, how many pencils and pens did she buy altogether?
Let x be the number of pencils and y be the number of pens Sally purchased. We are told that each pencil costs 25 cents. Because, the total amount she spent was given in dollars, we want to convert 25 cents to dollars. Because there are 100 cents in one dollar, 25 cents = \$0.25. Similarly, each pen costs \$0.50.
The amount that Sally spent on pencils is equal to the product of the number of pencils and the cost per pencil. We can model the amount of money spent on pencils as 0.25x.
Likewise, the amount Sally spent on pens is equal to the product of the number of pens and the cost per pen, or 0.5y.
Since we are told that Sally spent \$5.75 total on pens and pencils combined, we can write the following:

We are also told that the number of pens is one greater than the number of pencils. We can thus write:

We now have two equations and two unknowns. In order to solve this system of equations, we can take the value of y = x + 1 and substitute it into the other equation.

Distribute.

Combine x terms.

Subtract 0.5 from both sides.

Divide both sides by 0.75.

This means Sally bought 7 pencils and 8 pens. The question asks us to find the number of pens and pencils purchased altogether, which would equal

The answer is 15.
Let x be the number of pencils and y be the number of pens Sally purchased. We are told that each pencil costs 25 cents. Because, the total amount she spent was given in dollars, we want to convert 25 cents to dollars. Because there are 100 cents in one dollar, 25 cents = \$0.25. Similarly, each pen costs \$0.50.
The amount that Sally spent on pencils is equal to the product of the number of pencils and the cost per pencil. We can model the amount of money spent on pencils as 0.25x.
Likewise, the amount Sally spent on pens is equal to the product of the number of pens and the cost per pen, or 0.5y.
Since we are told that Sally spent \$5.75 total on pens and pencils combined, we can write the following:
We are also told that the number of pens is one greater than the number of pencils. We can thus write:
We now have two equations and two unknowns. In order to solve this system of equations, we can take the value of y = x + 1 and substitute it into the other equation.
Distribute.
Combine x terms.
Subtract 0.5 from both sides.
Divide both sides by 0.75.
This means Sally bought 7 pencils and 8 pens. The question asks us to find the number of pens and pencils purchased altogether, which would equal
The answer is 15.
Compare your answer with the correct one above


If  and
and  , what is the length of
, what is the length of  ?
?

If 


AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a  triangle, the opposites sides of those angles will be in the ratio
triangle, the opposites sides of those angles will be in the ratio  .
.
Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to  .
.




which also means

AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a 

Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to 
which also means
Compare your answer with the correct one above
Given:


How many solutions will there be for the system of equations?
Given:
How many solutions will there be for the system of equations?
Use the substitution method to solve the system of equations. There are two ways to do this - either substitute the first equation into the second, or the second equation into the first. Since the second equation is already solved for one variable, we will choose the latter.


Now factor the equation:

 or
or 
For this particular question, you could stop right here, as you can only need to know the number of solutions not the ordered pair of the solutions. Here there are two solutions. The ordered pairs would be:
 and
and 
Use the substitution method to solve the system of equations. There are two ways to do this - either substitute the first equation into the second, or the second equation into the first. Since the second equation is already solved for one variable, we will choose the latter.
Now factor the equation:

For this particular question, you could stop right here, as you can only need to know the number of solutions not the ordered pair of the solutions. Here there are two solutions. The ordered pairs would be:

Compare your answer with the correct one above



Find the value of  .
.
Find the value of 
Subtracting the second equation from the first, we acquire  .
.
Adding this equation to the third equation, we get  .
.
Therefore,  .
.
Subtracting the second equation from the first, we acquire 
Adding this equation to the third equation, we get 
Therefore, 
Compare your answer with the correct one above
Solve the following system of equations:


What is the sum of  and
and  ?
?
Solve the following system of equations:
What is the sum of 

This problem can be solved by using substitution. Write the first equation in terms of  and substitute it into the second equation.
and substitute it into the second equation.
So  and thus
and thus  and solving for
and solving for  and then
and then  .
.
So the sum of  and
and  is 7.
is 7.
This problem can be solved by using substitution. Write the first equation in terms of 
So 



So the sum of 

Compare your answer with the correct one above
George wants to paint the walls in his room blue. The ceilings are 10 ft tall and a carpet 12 ft by 15 ft covers the floor. One gallon of paint covers 400  and costs \$40. One quart of paint covers 100
and costs \$40. One quart of paint covers 100  and costs \$15. How much money will he spend on the blue paint?
and costs \$15. How much money will he spend on the blue paint?
George wants to paint the walls in his room blue. The ceilings are 10 ft tall and a carpet 12 ft by 15 ft covers the floor. One gallon of paint covers 400 

The area of the walls is given by 
One gallon of paint covers 400  and the remaining 140
and the remaining 140  would be covered by two quarts.
would be covered by two quarts.
So one gallon and two quarts of paint would cost 
The area of the walls is given by
One gallon of paint covers 400 

So one gallon and two quarts of paint would cost
Compare your answer with the correct one above
Simplify the radical expression.
![\sqrt[3]{-64x^{6}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26625/gif.latex)
Simplify the radical expression.
![\sqrt[3]{-64x^{6}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26625/gif.latex)
Look for perfect cubes within each term. This will allow us to factor out of the radical.
![\sqrt[3]{-64}*\sqrt[3]{x^6}*\sqrt[3]{y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/85063/gif.latex)
![\sqrt[3]{-4*-4*-4}*\sqrt[3]{x^2*x^2*x^2}*\sqrt[3]{y^4*y^4*y^4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/119850/gif.latex)
Simplify.

Look for perfect cubes within each term. This will allow us to factor out of the radical.
Simplify.
Compare your answer with the correct one above
Simplify the following expression:

Simplify the following expression:

This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.
Add like terms together:

 has no like terms.
has no like terms.

Combine these terms into one expression to find the answer:

This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.
Add like terms together:

Combine these terms into one expression to find the answer:
Compare your answer with the correct one above
Find the solution  to the system of equations.
to the system of equations.


Find the solution 
We can solve either by substitution or by elimination. We will solve by elimination.
Line up both equations so the variables are in the same order.


Because we have a negative  and a positive
and a positive  , if we were to add these two equations straight up and down, the
, if we were to add these two equations straight up and down, the  values would cancel out.
values would cancel out.


Solve for  .
.

Plug  back in to one of the original equations to solve for
back in to one of the original equations to solve for  .
.









The final answer will be  . We can check this answer by plugging it back into either of the original equations.
. We can check this answer by plugging it back into either of the original equations.
We can solve either by substitution or by elimination. We will solve by elimination.
Line up both equations so the variables are in the same order.
Because we have a negative 


Solve for 
Plug 





The final answer will be 
Compare your answer with the correct one above
Solve the system of equations.


Solve the system of equations.


For this system, it will be easiest to solve by substitution. The  variable is already isolated in the second equation. We can replace
variable is already isolated in the second equation. We can replace  in the first equation with
in the first equation with  , since these two values are equal.
, since these two values are equal.


Now we can solve for  .
.



Now that we know the value of  , we can solve for
, we can solve for  by using our original second equation.
by using our original second equation.



The final answer will be the ordered pair  .
.
For this system, it will be easiest to solve by substitution. The 


Now we can solve for 
Now that we know the value of 

The final answer will be the ordered pair 
Compare your answer with the correct one above
Define an operation  as follows:
as follows:
For all real numbers  ,
,

Evaluate 
Define an operation 
For all real numbers 
Evaluate
Compare your answer with the correct one above
Find the product:

Find the product:
Find the product:

Step 1: Use the distributive property.


Step 2: Combine like terms.


Find the product:
Step 1: Use the distributive property.
Step 2: Combine like terms.
Compare your answer with the correct one above







