Conversions - SAT Math
Card 0 of 164
How many  are in
are in 
How many 
To solve this problem we can make proportions.
We know that  and we can use
and we can use  as our unknown.
as our unknown.

Next, we want to cross multiply and divide to isolate the on one side.


The  will cancel and we are left with
will cancel and we are left with 
To solve this problem we can make proportions.
We know that 

Next, we want to cross multiply and divide to isolate the on one side.
The 
Compare your answer with the correct one above
How many  are in
are in 
How many 
To solve this problem we can make proportions.
We know that  and we can use
and we can use 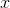 as our unknown.
as our unknown.

Next, we want to cross multiply and divide to isolate the on one side.


The  will cancel and we are left with
will cancel and we are left with 
To solve this problem we can make proportions.
We know that 
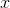
Next, we want to cross multiply and divide to isolate the on one side.
The 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown molding to use as accent pieces. He needs
of crown molding to use as accent pieces. He needs  of the molding for the house. How many feet of the material does he need to finish the model?
of the molding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many additional feet of the material will he need to purchase to finish the model?
of the moulding for the house. How many additional feet of the material will he need to purchase to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

The carpenter needs  of material. Since he already has
of material. Since he already has  he will need to purchase
he will need to purchase  more to finish the project.
more to finish the project.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 


Compare your answer with the correct one above
A carpenter is making a model house and he buys  of crown moulding to use as accent pieces. He needs
of crown moulding to use as accent pieces. He needs  of the moulding for the house. How many feet of the material does he need to finish the model?
of the moulding for the house. How many feet of the material does he need to finish the model?
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are  in
in  . We can write this relationship as the following ratio:
. We can write this relationship as the following ratio:

We know that the carpenter needs  of material to finish the house. We can write this as a ratio using the variable
of material to finish the house. We can write this as a ratio using the variable  to substitute the amount of feet.
to substitute the amount of feet.

Now, we can solve for  by creating a proportion using our two ratios.
by creating a proportion using our two ratios.

Cross multiply and solve for  .
.

Simplify.

Divide both sides by  .
.

Solve.

Reduce.

The carpenter needs  of material.
of material.
We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Compare your answer with the correct one above
Nancy is visiting her grandmother who lives  from her home. Her car’s tank has a full tank (
from her home. Her car’s tank has a full tank ( liters) at the beginning of her drive and uses
liters) at the beginning of her drive and uses  liter to drive
liter to drive  kilometers. How many liters will she need to refill to reach her grandmother’s house with
kilometers. How many liters will she need to refill to reach her grandmother’s house with  liters left in the tank?
liters left in the tank?
Nancy is visiting her grandmother who lives 




The correct answer is  liters.
liters.  .
.  .
.  .
.
The correct answer is 



Compare your answer with the correct one above
A future pharmacist is unsure what dose they should fill to ensure a patient takes a  -mg tablet
-mg tablet  times a day for one whole week. What is the total dosage they should prescribe?
times a day for one whole week. What is the total dosage they should prescribe?
A future pharmacist is unsure what dose they should fill to ensure a patient takes a 

The correct answer is  mg.
mg.  .
.
The correct answer is 

Compare your answer with the correct one above
A patient is prescribed  of a certain drug per day and is allowed to refill his prescription twice. If there are
of a certain drug per day and is allowed to refill his prescription twice. If there are  tablets in a prescription, and each tablet has
tablets in a prescription, and each tablet has  , how many doses are in the
, how many doses are in the  prescriptions (original +
prescriptions (original +  refills)?
refills)?
A patient is prescribed 




Compare your answer with the correct one above
A fruit farm produces strawberries and employs  workers. Each worker can pick
workers. Each worker can pick  pounds of berries per hour and work an
pounds of berries per hour and work an  -hour shift. If each pound of strawberries can be sold for
-hour shift. If each pound of strawberries can be sold for  , how much money does the farm make every day?
, how much money does the farm make every day?
A fruit farm produces strawberries and employs 



The key here is to ensure your units cancel out.  .
.
The key here is to ensure your units cancel out. 
Compare your answer with the correct one above
A record has a radius of  inches with the needle resting on the outer circumference of the record. If the record rotates at a speed of
inches with the needle resting on the outer circumference of the record. If the record rotates at a speed of  radians/sec and it takes
radians/sec and it takes  minutes to play a full song, how inches of track have been covered by the end of the song?
minutes to play a full song, how inches of track have been covered by the end of the song?
A record has a radius of 


Circumference  inches. The key here is to ensure your units cancel out.
inches. The key here is to ensure your units cancel out.  inch.
inch.
Circumference 

Compare your answer with the correct one above
A student was traveling  miles per hour. What is the student’s speed in feet per second?
miles per hour. What is the student’s speed in feet per second?
A student was traveling 
Compare your answer with the correct one above

