Coordinate Geometry - SAT Math
Card 0 of 2464
Which of the following could be a value of  for
for  ?
?
Which of the following could be a value of 

The graph is a down-opening parabola with a maximum of  . Therefore, there are no y values greater than this for this function.
. Therefore, there are no y values greater than this for this function.
The graph is a down-opening parabola with a maximum of 
Compare your answer with the correct one above

The figure above shows the graph of y = f(x). Which of the following is the graph of y = |f(x)|?
The figure above shows the graph of y = f(x). Which of the following is the graph of y = |f(x)|?
One of the properties of taking an absolute value of a function is that the values are all made positive. The values themselves do not change; only their signs do. In this graph, none of the y-values are negative, so none of them would change. Thus the two graphs should be identical.
One of the properties of taking an absolute value of a function is that the values are all made positive. The values themselves do not change; only their signs do. In this graph, none of the y-values are negative, so none of them would change. Thus the two graphs should be identical.
Compare your answer with the correct one above
Below is the graph of the function  :
:
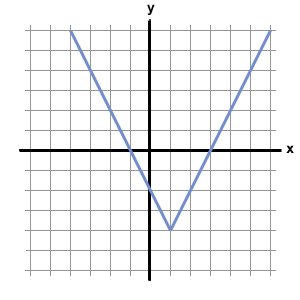
Which of the following could be the equation for  ?
?
Below is the graph of the function 

Which of the following could be the equation for 
First, because the graph consists of pieces that are straight lines, the function must include an absolute value, whose functions usually have a distinctive "V" shape. Thus, we can eliminate f(x) = x2 – 4x + 3 from our choices. Furthermore, functions with x2 terms are curved parabolas, and do not have straight line segments. This means that f(x) = |x2 – 4x| – 3 is not the correct choice.
Next, let's examine f(x) = |2x – 6|. Because this function consists of an abolute value by itself, its graph will not have any negative values. An absolute value by itself will only yield non-negative numbers. Therefore, because the graph dips below the x-axis (which means f(x) has negative values), f(x) = |2x – 6| cannot be the correct answer.
Next, we can analyze f(x) = |x – 1| – 2. Let's allow x to equal 1 and see what value we would obtain from f(1).
f(1) = | 1 – 1 | – 2 = 0 – 2 = –2
However, the graph above shows that f(1) = –4. As a result, f(x) = |x – 1| – 2 cannot be the correct equation for the function.
By process of elimination, the answer must be f(x) = |2x – 2| – 4. We can verify this by plugging in several values of x into this equation. For example f(1) = |2 – 2| – 4 = –4, which corresponds to the point (1, –4) on the graph above. Likewise, if we plug 3 or –1 into the equation f(x) = |2x – 2| – 4, we obtain zero, meaning that the graph should cross the x-axis at 3 and –1. According to the graph above, this is exactly what happens.
The answer is f(x) = |2x – 2| – 4.
First, because the graph consists of pieces that are straight lines, the function must include an absolute value, whose functions usually have a distinctive "V" shape. Thus, we can eliminate f(x) = x2 – 4x + 3 from our choices. Furthermore, functions with x2 terms are curved parabolas, and do not have straight line segments. This means that f(x) = |x2 – 4x| – 3 is not the correct choice.
Next, let's examine f(x) = |2x – 6|. Because this function consists of an abolute value by itself, its graph will not have any negative values. An absolute value by itself will only yield non-negative numbers. Therefore, because the graph dips below the x-axis (which means f(x) has negative values), f(x) = |2x – 6| cannot be the correct answer.
Next, we can analyze f(x) = |x – 1| – 2. Let's allow x to equal 1 and see what value we would obtain from f(1).
f(1) = | 1 – 1 | – 2 = 0 – 2 = –2
However, the graph above shows that f(1) = –4. As a result, f(x) = |x – 1| – 2 cannot be the correct equation for the function.
By process of elimination, the answer must be f(x) = |2x – 2| – 4. We can verify this by plugging in several values of x into this equation. For example f(1) = |2 – 2| – 4 = –4, which corresponds to the point (1, –4) on the graph above. Likewise, if we plug 3 or –1 into the equation f(x) = |2x – 2| – 4, we obtain zero, meaning that the graph should cross the x-axis at 3 and –1. According to the graph above, this is exactly what happens.
The answer is f(x) = |2x – 2| – 4.
Compare your answer with the correct one above

What is the equation for the line pictured above?

What is the equation for the line pictured above?
A line has the equation
 where
where  is the
is the  intercept and
intercept and  is the slope.
is the slope.
The  intercept can be found by noting the point where the line and the y-axis cross, in this case, at
intercept can be found by noting the point where the line and the y-axis cross, in this case, at  so
so  .
.
The slope can be found by selecting two points, for example, the y-intercept and the next point over that crosses an even point, for example,  .
.
Now applying the slope formula,

which yields  .
.
Therefore the equation of the line becomes:

A line has the equation




The 


The slope can be found by selecting two points, for example, the y-intercept and the next point over that crosses an even point, for example, 
Now applying the slope formula,
which yields 
Therefore the equation of the line becomes:
Compare your answer with the correct one above

Which of the following graphs represents the y-intercept of this function?
Which of the following graphs represents the y-intercept of this function?
Graphically, the y-intercept is the point at which the graph touches the y-axis. Algebraically, it is the value of  when
when  .
.
Here, we are given the function  . In order to calculate the y-intercept, set
. In order to calculate the y-intercept, set  equal to zero and solve for
equal to zero and solve for  .
.


So the y-intercept is at  .
.
Graphically, the y-intercept is the point at which the graph touches the y-axis. Algebraically, it is the value of 

Here, we are given the function 


So the y-intercept is at 
Compare your answer with the correct one above

Which of the following graphs represents the x-intercept of this function?
Which of the following graphs represents the x-intercept of this function?
Graphically, the x-intercept is the point at which the graph touches the x-axis. Algebraically, it is the value of  for which
for which  .
.
Here, we are given the function  . In order to calculate the x-intercept, set
. In order to calculate the x-intercept, set  equal to zero and solve for
equal to zero and solve for  .
.



So the x-intercept is at  .
.
Graphically, the x-intercept is the point at which the graph touches the x-axis. Algebraically, it is the value of 

Here, we are given the function 


So the x-intercept is at 
Compare your answer with the correct one above
Which of the following represents  ?
?
Which of the following represents 
A line is defined by any two points on the line. It is frequently simplest to calculate two points by substituting zero for x and solving for y, and by substituting zero for y and solving for x.

Let  . Then
. Then


So our first set of points (which is also the y-intercept) is 
Let  . Then
. Then



So our second set of points (which is also the x-intercept) is  .
.
A line is defined by any two points on the line. It is frequently simplest to calculate two points by substituting zero for x and solving for y, and by substituting zero for y and solving for x.
Let 
So our first set of points (which is also the y-intercept) is
Let 
So our second set of points (which is also the x-intercept) is 
Compare your answer with the correct one above
The graphic shows Bob's walk. At what times is Bob the furthest from home?

The graphic shows Bob's walk. At what times is Bob the furthest from home?

If we look at the graph, the line segment from  to
to  , is the furthest from home. So the answer will be from
, is the furthest from home. So the answer will be from  to
to  .
.
If we look at the graph, the line segment from 



Compare your answer with the correct one above
Let f(x) = -2x2 + 3x - 5. If g(x) represents f(x) after it has been shifted to the left by three units, and then shifted down by four, which of the following is equal to g(x)?
Let f(x) = -2x2 + 3x - 5. If g(x) represents f(x) after it has been shifted to the left by three units, and then shifted down by four, which of the following is equal to g(x)?
We are told that g(x) is found by taking f(x) and shifting it to the left by three and then down by four. This means that we can represent g(x) as follows:
g(x) = f(x + 3) - 4
Remember that the function f(x + 3) represents f(x) after it has been shifted to the LEFT by three, whereas f(x - 3) represents f(x) after being shifted to the RIGHT by three.
f(x) = -2x2 + 3x - 5
g(x) = f(x + 3) - 4 = \[-2(x+3)2 + 3(x+3) - 5\] - 4
g(x) = -2(x2 + 6x + 9) + 3x + 9 - 5 - 4
g(x) = -2x2 -12x -18 + 3x + 9 - 5 - 4
g(x) = -2x2 - 9x - 18 + 9 - 5 - 4
g(x) = -2x2 - 9x - 18
The answer is -2x2 - 9x - 18.
We are told that g(x) is found by taking f(x) and shifting it to the left by three and then down by four. This means that we can represent g(x) as follows:
g(x) = f(x + 3) - 4
Remember that the function f(x + 3) represents f(x) after it has been shifted to the LEFT by three, whereas f(x - 3) represents f(x) after being shifted to the RIGHT by three.
f(x) = -2x2 + 3x - 5
g(x) = f(x + 3) - 4 = \[-2(x+3)2 + 3(x+3) - 5\] - 4
g(x) = -2(x2 + 6x + 9) + 3x + 9 - 5 - 4
g(x) = -2x2 -12x -18 + 3x + 9 - 5 - 4
g(x) = -2x2 - 9x - 18 + 9 - 5 - 4
g(x) = -2x2 - 9x - 18
The answer is -2x2 - 9x - 18.
Compare your answer with the correct one above
Let f(x) = x3 – 2x2 + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?
Let f(x) = x3 – 2x2 + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?
In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.

Therefore, g(x) = f(–x).
f(x) = x3 – 2x2 + x – 4
g(x) = f(–x) = (–x)3 – 2(–x)2 + (–x) + 4
g(x) = (–1)3x3 –2(–1)2x2 – x + 4
g(x) = –x3 –2x2 –x + 4.
The answer is –x3 –2x2 –x + 4.
In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.

Therefore, g(x) = f(–x).
f(x) = x3 – 2x2 + x – 4
g(x) = f(–x) = (–x)3 – 2(–x)2 + (–x) + 4
g(x) = (–1)3x3 –2(–1)2x2 – x + 4
g(x) = –x3 –2x2 –x + 4.
The answer is –x3 –2x2 –x + 4.
Compare your answer with the correct one above
Line m passes through the points (–4, 3) and (2, –6). If line q is generated by reflecting m across the line y = x, then which of the following represents the equation of q?
Line m passes through the points (–4, 3) and (2, –6). If line q is generated by reflecting m across the line y = x, then which of the following represents the equation of q?
When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a).
Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2).
Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.
First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x1, y1) and (x2, y2).
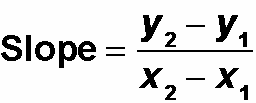
slope = (2 – (–4))/(–6 –3)
= 6/–9 = –2/3
Next, we can use the point-slope formula to find the equation for q.
y – y1 = slope(x – x1)
y – 2 = (–2/3)(x – (–6))
Multiply both sides by 3.
3(y – 2) = –2(x + 6)
3y – 6 = –2x – 12
Add 2x to both sides.
2x + 3y – 6 = –12
Add six to both sides.
2x + 3y = –6
The answer is 2x + 3y = –6.
When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a).
Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2).
Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.
First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x1, y1) and (x2, y2).
slope = (2 – (–4))/(–6 –3)
= 6/–9 = –2/3
Next, we can use the point-slope formula to find the equation for q.
y – y1 = slope(x – x1)
y – 2 = (–2/3)(x – (–6))
Multiply both sides by 3.
3(y – 2) = –2(x + 6)
3y – 6 = –2x – 12
Add 2x to both sides.
2x + 3y – 6 = –12
Add six to both sides.
2x + 3y = –6
The answer is 2x + 3y = –6.
Compare your answer with the correct one above
Let f(x) be a function. Which of the following represents f(x) after it has been reflected across the x-axis, then shifted to the left by four units, and then shifted down by five units?
Let f(x) be a function. Which of the following represents f(x) after it has been reflected across the x-axis, then shifted to the left by four units, and then shifted down by five units?
f(x) undergoes a series of three transformations. The first transformation is the reflection of f(x) across the x-axis. This kind of transformation takes all of the negative values and makes them positive, and all of the positive values and makes them negative. This can be represented by multiplying f(x) by –1. Thus, –f(x) represents f(x) after it is reflected across the x-axis.
Next, the function is shifted to the left by four. In general, if g(x) is a function, then g(x – h) represents a shift by h units. If h is positive, then the shift is to the right, and if h is negative, then the shift is to the left. In order, to shift the function to the left by four, we would need to let h = –4. Thus, after –f(x) is shifted to the left by four, we can write this as –f(x – (–4)) = –f(x + 4).
The final transformation requires shifting the function down by 5. In general, if g(x) is a function, then g(x) + h represents a shift upward if h is positive and a shift downward if h is negative. Thus, a downward shift of 5 to the function –f(x + 4) would be represented as –f(x + 4) – 5.
The three transformations of f(x) can be represented as –f(x + 4) – 5.
The answer is –f(x + 4) – 5.
f(x) undergoes a series of three transformations. The first transformation is the reflection of f(x) across the x-axis. This kind of transformation takes all of the negative values and makes them positive, and all of the positive values and makes them negative. This can be represented by multiplying f(x) by –1. Thus, –f(x) represents f(x) after it is reflected across the x-axis.
Next, the function is shifted to the left by four. In general, if g(x) is a function, then g(x – h) represents a shift by h units. If h is positive, then the shift is to the right, and if h is negative, then the shift is to the left. In order, to shift the function to the left by four, we would need to let h = –4. Thus, after –f(x) is shifted to the left by four, we can write this as –f(x – (–4)) = –f(x + 4).
The final transformation requires shifting the function down by 5. In general, if g(x) is a function, then g(x) + h represents a shift upward if h is positive and a shift downward if h is negative. Thus, a downward shift of 5 to the function –f(x + 4) would be represented as –f(x + 4) – 5.
The three transformations of f(x) can be represented as –f(x + 4) – 5.
The answer is –f(x + 4) – 5.
Compare your answer with the correct one above

Refer to the above diagram.
True or false:  and
and  comprise a linear pair.
comprise a linear pair.

Refer to the above diagram.
True or false: 

By definition, two angles form a linear pair if and only if
(1) they have the same vertex;
(2) they share a side; and,
(3) their interiors have no points in common.
In the figure below,  and
and  are marked in green and red, respectively:
are marked in green and red, respectively:

The two angles have the same vertex and share no interior points. However, they do not share a side. Therefore, they do not comprise a linear pair.
By definition, two angles form a linear pair if and only if
(1) they have the same vertex;
(2) they share a side; and,
(3) their interiors have no points in common.
In the figure below, 


The two angles have the same vertex and share no interior points. However, they do not share a side. Therefore, they do not comprise a linear pair.
Compare your answer with the correct one above

The graphs of  and
and  are shown above. Which equation best describes the relationship between
are shown above. Which equation best describes the relationship between  and
and  ?
?
The graphs of 



Compare your answer with the correct one above
If the point (6, 7) is reflected over the line  and then over the x-axis, what is the resulting coordinate?
and then over the x-axis, what is the resulting coordinate?
If the point (6, 7) is reflected over the line 
A reflection over the line  involves a switching of the coordinates to get us (7, 6). A reflection over the x-axis involves a negation of the y-coordinate. Thus the resulting point is (7, –6).
involves a switching of the coordinates to get us (7, 6). A reflection over the x-axis involves a negation of the y-coordinate. Thus the resulting point is (7, –6).
A reflection over the line 
Compare your answer with the correct one above
You are looking at a map of your town and your house is located at the coordinate (0,0). Your school is located at the point (3,4). If each coordinate distance is 1.3 miles, how far away is your school?
You are looking at a map of your town and your house is located at the coordinate (0,0). Your school is located at the point (3,4). If each coordinate distance is 1.3 miles, how far away is your school?
The coordinate length between you and your school is equivalent to the hypotenuse of a right triangle with sides of 3 and 4 units:




The distance is 5 coordinate lengths, and each coordinate length corresponds to 1.3 miles of distance, so

The coordinate length between you and your school is equivalent to the hypotenuse of a right triangle with sides of 3 and 4 units:
The distance is 5 coordinate lengths, and each coordinate length corresponds to 1.3 miles of distance, so
Compare your answer with the correct one above
Solve each problem and decide which is the best of the choices given.
What is the amplitude of the following function?

Solve each problem and decide which is the best of the choices given.
What is the amplitude of the following function?
The amplitude is always the number in front of the trig function  .
.
The general equation to remember is,

where
 is amplitude
is amplitude
 is period of
is period of  and
and
 is the phase shift.
is the phase shift.
In this case it's  .
.
The amplitude is always the number in front of the trig function 
The general equation to remember is,
where




In this case it's 
Compare your answer with the correct one above

Refer to the above figure.
True or false:  and
and  comprise a pair of opposite rays.
comprise a pair of opposite rays.

Refer to the above figure.
True or false: 

Two rays are opposite rays, by definition, if
(1) they have the same endpoint, and
(2) their union is a line.
The first letter in the name of a ray refers to its endpoint; the second refers to the name of any other point on the ray.  and
and  both have endpoint
both have endpoint  , so the first criterion is met.
, so the first criterion is met.  passes through point
passes through point  and
and  passes through point
passes through point  ;
;  and
and  are indicated below in green and red, respectively:
are indicated below in green and red, respectively:

The union of the two rays is a line. Both criteria are met, so the rays are indeed opposite.
Two rays are opposite rays, by definition, if
(1) they have the same endpoint, and
(2) their union is a line.
The first letter in the name of a ray refers to its endpoint; the second refers to the name of any other point on the ray. 









The union of the two rays is a line. Both criteria are met, so the rays are indeed opposite.
Compare your answer with the correct one above
The following is an equation of a circle:

If this circle is moved to the left 2 spaces and down 3 spaces, where does the center of the new circle lie?
The following is an equation of a circle:
If this circle is moved to the left 2 spaces and down 3 spaces, where does the center of the new circle lie?
The general formula for a circle with center (h,k) and radius r is  .
.
The center of the original circle, therefore, is (2, -4).
If we move the circle to the left 2 spaces and down 3 spaces, then the center of the new circle is given by  or
or  .
.
The general formula for a circle with center (h,k) and radius r is 
The center of the original circle, therefore, is (2, -4).
If we move the circle to the left 2 spaces and down 3 spaces, then the center of the new circle is given by 

Compare your answer with the correct one above
Bobby draws a circle on graph paper with a center at (2, 5) and a radius of 10.
Jenny moves Bobby's circle up 2 units and to the right 1 unit.
What is the equation of Jenny's circle?
Bobby draws a circle on graph paper with a center at (2, 5) and a radius of 10.
Jenny moves Bobby's circle up 2 units and to the right 1 unit.
What is the equation of Jenny's circle?
If Jenny moves Bobby's circle up 2 units and to the right 1 unit, then the center of her circle is (3, 7). The radius remains 10.
The general equation for a circle with center (h, k) and radius r is given by

For Jenny's circle, (h, k) = (3, 7) and r=10.
Substituting these values into the general equation gives us

If Jenny moves Bobby's circle up 2 units and to the right 1 unit, then the center of her circle is (3, 7). The radius remains 10.
The general equation for a circle with center (h, k) and radius r is given by
For Jenny's circle, (h, k) = (3, 7) and r=10.
Substituting these values into the general equation gives us
Compare your answer with the correct one above

